Surface aggregation patterns of LDL receptors near coated pits III: potential effects of combined retrograde membrane flow-diffusion and a polarized-insertion mechanism

Abstract

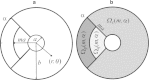
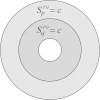
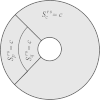
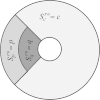
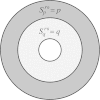
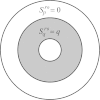
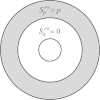
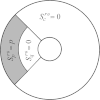
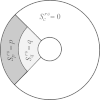
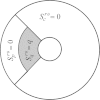
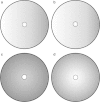
Although the process of endocytosis of the low density lipoprotein (LDL) macromolecule and its receptor have been the subject of intense experimental research and modeling, there are still conflicting hypotheses and even conflicting data regarding the way receptors are transported to coated pits, the manner by which receptors are inserted before they aggregate in coated pits, and the display of receptors on the cell surface. At first it was considered that LDL receptors in human fibroblasts are inserted at random locations and then transported by diffusion toward coated pits. But experiments have not ruled out the possibility that the true rate of accumulation of LDL receptors in coated pits might be faster than predicted on the basis of pure diffusion and uniform reinsertion over the entire cell surface. It has been claimed that recycled LDL receptors are inserted preferentially in regions where coated pits form, with display occurring predominantly as groups of loosely associated units. Another mechanism that has been proposed by experimental cell biologists which might affect the accumulation of receptors in coated pits is a retrograde membrane flow. This is essentially linked to a polarized receptor insertion mode and also to the capping phenomenon, characterized by the formation of large patches of proteins that passively flow away from the regions of membrane exocytosis. In this contribution we calculate the mean travel time of LDL receptors to coated pits as determined by the ratio of flow strength to diffusion-coefficient, as well as by polarized-receptor insertion. We also project the resulting display of unbound receptors on the cell membrane. We found forms of polarized insertion that could potentially reduce the mean capture time of LDL receptors by coated pits which is controlled by diffusion and uniform insertion. Our results show that, in spite of its efficiency as a possible device for enhancement of the rate of receptor trapping, polarized insertion nevertheless fails to induce the formation of steady-state clusters of receptor on the cell membrane. Moreover, for appropriate values of the flow strength-diffusion ratio, the predicted steady-state distribution of receptors on the surface was found to be consistent with the phenomenon of capping.

Figure 1

The geometry of the model. a) A circular trap of radius a (the coated pit) is encircled by an annulus of radius b (the reference region Ω associated with a coated pit). LDL receptors originally inserted at a point (r, θ) inside the reference annulus Ω, move afterwards by convection and diffusion until they are trapped in coated pits. b) Receptor insertion occurs according to a partitioned insertion rate function S^rθ(c, p, q, m, α), which sorts receptors at distinct rates $S_c^{\mathit{r\theta }}\left(m,\alpha \right)$, $S_p^{\mathit{r\theta }}\left(m,\alpha \right)$ and $S_q^{\mathit{r\theta }}\left(m,\alpha \right)$ linked respectively to the disjoint regions Ω_c, Ω_p and Ω_q.

Figure 2

The c-uniform insertion mode. A receptor insertion mechanism symbolized here by means of S^rθ(c, 0, 0, b/a, 0), which is obtained by setting $S_p^{\mathit{r\theta }}\left(\mathit{b}/\mathit{a},0\right)=S_q^{\mathit{r\theta }}\left(\mathit{m},\mathit{\alpha }\right)=0$ and $S_c^{\mathit{r\theta }}\left(\mathit{b}/\mathit{a},0\right)=\mathit{c}$, with c a positive constant.

Figure 3

The pq-uniform insertion mode. This is denoted by means of the symbol S^rθ(0, c, c, m, π), and obtained by setting the conditions $S_c^{\mathit{r\theta }}\left(m,\pi \right)=0$ and $S_p^{\mathit{r\theta }}\left(m,\pi \right)=S_q^{\mathit{r\theta }}\left(m,\pi \right)=c$, with c a positive constant.

Figure 4

The cpq-uniform insertion mode. A device symbolized here using S^rθ(c, c, c, m, α) and is obtained by setting $S_c^{\mathit{r\theta }}\left(m,\alpha \right)=S_p^{\mathit{r\theta }}\left(m,\alpha \right)=S_q^{\mathit{r\theta }}\left(m,\alpha \right)=c$, with c a positive constant.

Figure 5

The cpq-locally uniform insertion mode. This insertion rate function is labeled by means of S^rθ(c, p, q, m, α), it is linked to the conditions $S_c^{\mathit{r\theta }}\left(m,\alpha \right)=c$, $S_p^{\mathit{r\theta }}\left(m,\alpha \right)=p$, and $S_q^{\mathit{r\theta }}\left(m,\alpha \right)=q$, with c, p and q positive constants.

Figure 6

The pq-locally uniform insertion mode. A receptor insertion mechanism which is denoted by means of S^rθ(0, p, q, m, π). It is radially symmetric over each one of the regions Ω_p and Ω_q. This form is associated with the case $S_c^{\mathit{r\theta }}\left(m,\pi \right)=0$, $S_p^{\mathit{r\theta }}\left(m,\pi \right)=p$, and $S_q^{\mathit{r\theta }}\left(m,\pi \right)=q$, with p and q positive constants.

Figure 7

The q-plaque form insertion mode. This mode is denoted here by means of the symbol S^rθ(0, 0, q, m, π). It is radially symmetric and polarized and associated with the conditions $S_c^{\mathit{r\theta }}\left(m,\pi \right)=0$, $S_p^{\mathit{r\theta }}\left(m,\pi \right)=0$, and $S_q^{\mathit{r\theta }}\left(m,\pi \right)=q$, with q a positive constant.

Figure 8

The p-peripheral insertion mode. An insertion form denoted here by means of S^rθ(0, p, 0, m, π). It is a radially symmetric and polarized and linked to the case $S_c^{\mathit{r\theta }}\left(m,\pi \right)=0$, $S_p^{\mathit{r\theta }}\left(m,\pi \right)=p$, and $S_q^{\mathit{r\theta }}\left(m,\pi \right)=0$, with p a positive constant.

Figure 9

The p-polarized insertion mode. This form is symbolized here by S^rθ(0, p, 0, m, α) and obtained by setting $S_c^{\mathit{r\theta }}\left(m,\alpha \right)=0$, $S_p^{\mathit{r\theta }}\left(m,\alpha \right)=p$, $S_q^{\mathit{r\theta }}\left(m,\alpha \right)=0$, with p a positive constant. Under the condition λ = v₁/2D₀, which determines capping, this mode was found to produce values for τ_λma that are equivalent to τ_du.

Figure 10

The pq-polarized insertion mode. This insertion mechanism is denoted here through S^rθ(0, p, q, m, α). It is polarized and non-radially symmetric and linked to the conditions $S_c^{\mathit{r\theta }}\left(m,\alpha \right)=0$, $S_p^{\mathit{r\theta }}\left(m,\alpha \right)=p$,and $S_q^{\mathit{r\theta }}\left(m,\alpha \right)=q$, with p and q as positive constant. Even for λ = v₁/2D₀, which produce capping-like effects, certain characterization of this mode can give substantial reductions in τ_du.

Figure 11

The q-polarized insertion mode. A receptor insertion paradigm denoted here by means of S^rθ(0, 0, q, m, α) is linked to the case $S_c^{\mathit{r\theta }}\left(m,\alpha \right)=0$, $S_p^{\mathit{r\theta }}\left(m,\alpha \right)=0$, and $S_q^{\mathit{r\theta }}\left(m,\alpha \right)=q$, with q a positive constant. This mode is non-radially symmetric and polarized. Setting = π , the q-polarized insertion mode gives the paradigm of Wofsy et al. [35] for insertion in plaques. Even when λ = v₁/2D₀ holds so that the capping phenomenon could create a graduated distribution of unbound receptors in the direction of flow streamlines, this mode seems to provide a highly efficient form of receptor insertion by making dramatic reductions on τ_du.

Figure 12

Surface aggregation patterns of unbound LDL receptors associated with different values of the fundamental ratio λ and non-radially symmetric-polarized insertion modes. a) the surface pattern made by λ = v₁/2D₀ and the q-polarized insertion mode S^rθ(0, 0, q, m, α), with m = 2.3, δ_q(m, α) = 1 and α = π/4; b) surface pattern associated with the case λ = v₁/2D₁ and the p-polarized insertion mode S^rθ(0, p, 0, m, α) with α = π/6, m = 9.5, and δ_p(m, α) = 1; c) the surface aggregation pattern formed by λ = v₁/2D_ext and q-polarized insertion S^rθ(0, p, q, m, α) with m = 1.2, α = π/6 and δ_q(m, α) = 1; d) the surface receptor pattern for λ = v₁/2D_ext and p-polarized insertion S^rθ(0, p, q, m, α) with m = 9.5, α = π/4 and δ_p(m, α) = 1. The patterns shown are consistent with the capping phenomena; that is, when convection is fast (v = v₁) and diffusion is normal (D = D₀) a graduated distribution in the direction of flow streamlines is observed, a) and b). But in the presence of a fast convective transport, suitable values of the diffusion coefficient (e. g. D = D_ext) can reverse the capping effect and induce an effective randomization of the distribution of unbound LDL receptors, c) and d). In any event, in the presence of a retrograde membrane flow, no receptor surface clusters are formed.