Aspiration-based partner switching boosts cooperation in social dilemmas
- PMID: 24896269
- PMCID: PMC4045582
- DOI: 10.1371/journal.pone.0097866
Aspiration-based partner switching boosts cooperation in social dilemmas
Abstract
Most previous studies concerning linking dynamics often assumed that links pairing individuals should be identified and treated differently during topology adjusting procedure, in order to promote cooperation. A common assumption was that cooperators were expected to avoid being exploited by quickly breaking up relationships with defectors. Then the so-called prosocial links linking two cooperators (abbreviated as CC links hereafter) would be much favored by evolution, whereby cooperation was promoted. However, we suggest that this is not always necessary. Here, we developed a minimal model in which an aspiration-based partner switching mechanism was embedded to regulate the evolution of cooperation in social dilemmas. Individuals adjusted social ties in a self-questioning manner in line with the learning theory. Less game information was involved during dynamic linking and all links were tackled anonymously irrespective of their types (i.e., CD links, DD links, or CC links). The main results indicate that cooperation flourishes for a broad range of parameters. The denser the underlying network, the more difficult the evolution of cooperation. More importantly, moderate aspirations do much better in promoting the evolution of altruistic behavior and for most cases there exists the optimal aspiration level that most benefits cooperation. Too strong or too weak selection intensity turns out to be pretty conducive to the evolution of cooperation in such a dynamical system.
Conflict of interest statement
Figures
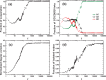
 , (d) fraction of isolated nodes. Here, individuals adaptively adjust social ties in a self-questioning way based on the learning theory, and less information concerning strategies is involved during the partner switching process. Even so, this simple and smart mechanism successfully drives the system to the full cooperation state without spying on the types of links as well as the types of individuals. Initially, each individual is randomly designated as a cooperator or a defector with equal probability and all individuals are uniformly distributed in the network. Other parameters:
, (d) fraction of isolated nodes. Here, individuals adaptively adjust social ties in a self-questioning way based on the learning theory, and less information concerning strategies is involved during the partner switching process. Even so, this simple and smart mechanism successfully drives the system to the full cooperation state without spying on the types of links as well as the types of individuals. Initially, each individual is randomly designated as a cooperator or a defector with equal probability and all individuals are uniformly distributed in the network. Other parameters:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 . Other parameters and conditions are the same as in Fig. 1.
. Other parameters and conditions are the same as in Fig. 1.
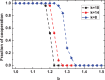
 corresponds to the results obtained on static networks. Based on this plot, one can conclude that the aspiration level plays a crucial role in the evolution of cooperation. Moderate aspirations are more efficient in terms of boosting cooperation.
corresponds to the results obtained on static networks. Based on this plot, one can conclude that the aspiration level plays a crucial role in the evolution of cooperation. Moderate aspirations are more efficient in terms of boosting cooperation.  for the PDG (a), and for the SG
for the PDG (a), and for the SG  (b). Other parameters and conditions are the same as in Fig. 1.
(b). Other parameters and conditions are the same as in Fig. 1.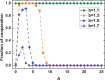
 corresponds to the results obtained on static networks. It reflects that the influences of
corresponds to the results obtained on static networks. It reflects that the influences of  on cooperation relay closely on the challenge that cooperation is facing. For most values of
on cooperation relay closely on the challenge that cooperation is facing. For most values of  , there exists the optimal
, there exists the optimal  that most fosters cooperation. Other parameters and conditions are the same as in Fig. 1.
that most fosters cooperation. Other parameters and conditions are the same as in Fig. 1.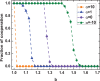
 corresponds to random partner selection in determining which one to dismiss. The plot indicates that rewiring connections with the poorer partners can often benefit the evolution of cooperation. And the smaller the value of
corresponds to random partner selection in determining which one to dismiss. The plot indicates that rewiring connections with the poorer partners can often benefit the evolution of cooperation. And the smaller the value of  , the stronger the promotion of cooperation.
, the stronger the promotion of cooperation.  . Other parameters and conditions are the same as in Fig. 1.
. Other parameters and conditions are the same as in Fig. 1.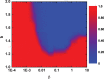
 and
and  is plotted in this figure. It shows that cooperation thrives under either very strong or very weak selection strength. Particularly, for
is plotted in this figure. It shows that cooperation thrives under either very strong or very weak selection strength. Particularly, for  the full cooperation state can be kept in the whole range of
the full cooperation state can be kept in the whole range of  . Moreover, the approximate U-shaped curve implies that there exists the worst
. Moreover, the approximate U-shaped curve implies that there exists the worst  that extremely inhibits the evolution of altruism.
that extremely inhibits the evolution of altruism.  . Other parameters and conditions are the same as in Fig. 1.
. Other parameters and conditions are the same as in Fig. 1.References
-
- Coleman JS (1990) Foundations of social theory. Cambridge, MA: Harvard University Press.
-
- Nowak MA, May RM (1992) Evolutionary games and spatial chaos. Nature 359: 826–829.
-
- Nowak MA, Sigmund K (1993) A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner’s Dilemma game. Nature 364: 56–58. - PubMed
-
- Traulsen A, Claussen JC, Hauert C (2005) Coevolutionary dynamics: from finite to infinite populations. Phys Rev Lett 95: 238701. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

