Mechanics and spiral formation in the rat cornea

Abstract

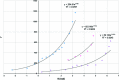
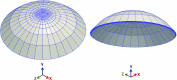
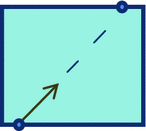
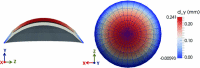
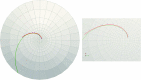
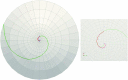
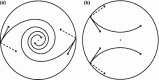
During the maturation of some mammals such as mice and rats, corneal epithelial cells tend to develop into patterns such as spirals over time. A better understanding of these patterns can help to understand how the organ develops and may give insight into some of the diseases affecting corneal development. In this paper, a framework for explaining the development of the epithelial cells forming spiral patterns due to the effect of tensile and shear strains is proposed. Using chimeric animals, made by combining embryonic cells from genetically distinguishable strains, we can observe the development of patterns in the cornea. Aggregates of cell progeny from one strain or the other called patches form as organs and tissue develop. The boundaries of these patches are fitted with logarithmic spirals on confocal images of adult rat corneas. To compare with observed patterns, we develop a three-dimensional large strain finite element model for the rat cornea under intraocular pressure to examine the strain distribution on the cornea surface. The model includes the effects of oriented and dispersed fibrils families throughout the cornea and a nearly incompressible matrix. Tracing the directions of critical strain vectors on the cornea surface leads to spiral-like curves that are compared to the observed logarithmic spirals. Good agreement between the observed and numerical curves supports the proposed assumption that shear and tensile strains facilitate sliding of epithelial cells to develop spiral patterns.

Fig. 1

Confocal images of cornea from a 10-month-old rat (C1), b 13-month-old rat (C2), c, d 16-month-old rat (C3-1 and C3-2, right and left corneas of the same animal, respectively). For each rat cornea, three sets of landmarks are overlaid along the cell boundaries that resemble spiral patterns. These points are fitted with logarithmic spirals (red curves), and the pitch angles are measured. Scale bars on each cornea are $500\mathrm{\mu }\text{m}$

Fig. 2

$r$ versus $\mathit{\theta }$ plot of landmark points and the matching logarithmic spirals in the polar coordinates for sampling cornea C3-1

Fig. 3

Schematic representation of pitch angle of a logarithmic spiral

Fig. 4

Confocal image of cross section of a rat cornea used to construct the geometry of the cornea for the finite element model (Iannaccone et al. 2012). In the zoomed-in image, Epi. is the epithelium, Str. is the stroma, and End. is the endothelium

Fig. 5

Two-dimensional representation of geometry used to create the three-dimensional structure of the rat cornea

Fig. 6

Schematic of superior–inferior and nasal–temporal directions (Meek et al. 1987)

Fig. 7

Schematic presentation of the assumed predominant directions of collagen fibrils in the rat cornea for numerical purposes. The collagen fibrils are assumed to have varying preferred orientations depending on the three regions defined on the cornea: central area, transition zone, and corneal edge

Fig. 8

Three-dimensional representation of the 10-layered rat cornea mesh having 4480 elements using tri-linear averaged volume $\overline{\mathit{B}}$ hexahedral elements

Fig. 9

Schematic two-dimensional representation of the approach used for finding the endpoints at each element

Fig. 10

Vertical displacement mapping of the rat cornea subjected to IOP is shown in cross section on the left and on the top surface on the right. In the left picture, the gray surface is the undeformed shape of the cornea and vertical displacement colored by magnitude is shown in top

Fig. 11

Cornea C1: landmark points overlaid onto the cell boundaries are shown in blue, the logarithmic spiral with $-42.7^{\circ }$ pitch angle fitted to the landmarks is shown in red, and green curve is obtained from FE simulations ($c$ = 1). The figure on the right demonstrates the zoomed-in view of the central part of the rat cornea on the left

Fig. 12

Cornea C2: landmark points overlaid onto the cell boundaries are shown in blue, the logarithmic spiral with $32.5^{\circ }$ pitch angle fitted to the landmarks is shown in red, and green curve is obtained from FE simulations ($c$ = 1.45). The figure on the right demonstrates the zoomed-in view of the central part of the rat cornea on the left

Fig. 13

Cornea C3-1: landmark points overlaid onto the cell boundaries are shown in blue, the logarithmic spiral with $23.4^{\circ }$ pitch angle fitted to the landmarks is shown in red, and green curve is obtained from FE simulations ($c$ = 2). The figure on the right demonstrates the zoomed-in view of the central part of the rat cornea on the left

Fig. 14

Cornea C3-2: landmark points overlaid onto the cell boundaries are shown in blue, the logarithmic spiral with ${24}^{\circ }$ pitch angle fitted to the landmarks is shown in red, and green curve is obtained from FE simulations ($c$ = 2). The figure on the right demonstrates the zoomed-in view of the central part of the rat cornea on the left

Fig. 15

a Mohr’s circle showing the critical surface traction, located at $\frac{\mathit{\pi }}{2}-\mathit{\alpha }$ from the major principal strain on Mohr’s circle, or half that in physical space. b Critical direction in physical space as a function of the principal directions

Fig. 16

a If the majority of cells in all parts of the cornea tend to slip in one dominant direction, clockwise or counterclockwise, the cells will spiral. b If cells in one section start to slide in a different direction that other cells, different patterns, such as horseshoes, can emerge