Weighted multiplex networks
- PMID: 24906003
- PMCID: PMC4048161
- DOI: 10.1371/journal.pone.0097857
Weighted multiplex networks
Abstract
One of the most important challenges in network science is to quantify the information encoded in complex network structures. Disentangling randomness from organizational principles is even more demanding when networks have a multiplex nature. Multiplex networks are multilayer systems of [Formula: see text] nodes that can be linked in multiple interacting and co-evolving layers. In these networks, relevant information might not be captured if the single layers were analyzed separately. Here we demonstrate that such partial analysis of layers fails to capture significant correlations between weights and topology of complex multiplex networks. To this end, we study two weighted multiplex co-authorship and citation networks involving the authors included in the American Physical Society. We show that in these networks weights are strongly correlated with multiplex structure, and provide empirical evidence in favor of the advantage of studying weighted measures of multiplex networks, such as multistrength and the inverse multiparticipation ratio. Finally, we introduce a theoretical framework based on the entropy of multiplex ensembles to quantify the information stored in multiplex networks that would remain undetected if the single layers were analyzed in isolation.
Conflict of interest statement
Figures
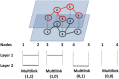
 and
and  are linked by one multilink
are linked by one multilink  .
.
 defined in Eq. (8) are the same, while exponents
defined in Eq. (8) are the same, while exponents  are significantly different. Similar results can be obtained for the exponents in the PRE collaboration layer. Nevertheless, multistrengths
are significantly different. Similar results can be obtained for the exponents in the PRE collaboration layer. Nevertheless, multistrengths  are always larger than multistrengths
are always larger than multistrengths  and
and  , when multistrengths are calculated over the same number of multilinks, i.e.,
, when multistrengths are calculated over the same number of multilinks, i.e.,  (see Text S1 for the statistical test on this hypothesis).
(see Text S1 for the statistical test on this hypothesis).
 is larger than the average weight of multilinks
is larger than the average weight of multilinks  . Moreover, the exponents
. Moreover, the exponents  ,
,  are larger than exponents
are larger than exponents  . In the case of the citation layer, both the incoming multistrengths and the outgoing multistrengths have a functional behavior that varies depending on the type of multilink. Conversely, the average inverse multiparticipation ratio in the citation layer does not show any significant change of behavior when compared across different multilinks.
. In the case of the citation layer, both the incoming multistrengths and the outgoing multistrengths have a functional behavior that varies depending on the type of multilink. Conversely, the average inverse multiparticipation ratio in the citation layer does not show any significant change of behavior when compared across different multilinks.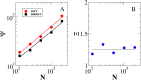
 nodes with respect to a null model in which the weights are distributed uniformly over the multiplex network. (B) Value of the indicator
nodes with respect to a null model in which the weights are distributed uniformly over the multiplex network. (B) Value of the indicator  defined in Eq. (12) indicating the additional amount of information encoded in the properties of multilinks in the correlated multiplex ensemble with respect to the corresponding uncorrelated multiplex ensemble. The solid line refers to the average value of
defined in Eq. (12) indicating the additional amount of information encoded in the properties of multilinks in the correlated multiplex ensemble with respect to the corresponding uncorrelated multiplex ensemble. The solid line refers to the average value of  over the different multiplex network sizes.
over the different multiplex network sizes.References
-
- Albert R, Barabási A-L (2002) Statistical mechanics of complex networks. Reviews of Modern Physics 74: 47–97.
-
- Newman MEJ (2003) Structure and function of complex networks. SIAM Review 45: 167–256.
-
- Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D-U (2006) Complex networks: Structure and dynamics. Physics Reports 424: 175–308.
-
- Fortunato S (2010) Community detection in graphs. Physics Reports 486: 75–174.
-
- Kivelä M, Arenas A, Barthélemy M, Gleeson JP, Moreno Y, et al... (2013) Multilayer networks. arXiv: 1309.7233.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

