Navigability of interconnected networks under random failures

Abstract

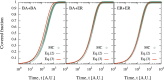
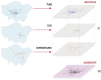
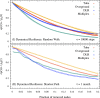
Assessing the navigability of interconnected networks (transporting information, people, or goods) under eventual random failures is of utmost importance to design and protect critical infrastructures. Random walks are a good proxy to determine this navigability, specifically the coverage time of random walks, which is a measure of the dynamical functionality of the network. Here, we introduce the theoretical tools required to describe random walks in interconnected networks accounting for structure and dynamics inherent to real systems. We develop an analytical approach for the covering time of random walks in interconnected networks and compare it with extensive Monte Carlo simulations. Generally speaking, interconnected networks are more resilient to random failures than their individual layers per se, and we are able to quantify this effect. As an application--which we illustrate by considering the public transport of London--we show how the efficiency in exploring the multiplex critically depends on layers' topology, interconnection strengths, and walk strategy. Our findings are corroborated by data-driven simulations, where the empirical distribution of check-ins and checks-out is considered and passengers travel along fastest paths in a network affected by real disruptions. These findings are fundamental for further development of searching and navigability strategies in real interconnected systems.

Fig. 1.

Example of the navigation on an interconnected network. Path (dotted red line) of a random walker exploiting the multiplex topology to find a way around to jump between disconnected components. In this example the walker is not allowed to switch between layer 1 and layer 3 in one time step.

Fig. 2.

Theoretical description of the navigability of a multiplex against simulation. Coverage versus time obtained from Monte Carlo simulations and our theoretical predictions given by Eqs. 2 and 3. A two-layer multiplex with $D_X=D^{11}=D^{22}=1$ is considered.

Fig. 3.

Multilayer network of public transport of London. (I) Tube, overground, and DLR define three layers of the multiplex transportation network. Each station, individuated by a geographical position, represents a vertex, whereas the existence of a real connection between two stations defines the presence of an edge. (II) Aggregate network corresponding to the weighted projection of the multiplex to a single-layer graph, where the information about the type of transport is lost.

Fig. 4.

Resilience of the public transport network of London to random failures. (I) Theoretical expectations (solid lines) reproduce with great accuracy the resilience (points) obtained from simulations for each transportation layer and the whole interconnected system $\left(D_X={10}^{-1}\right)$, assuming random-walk-based navigation. (II) The same as I but assuming shortest-path-based navigation and empirical data.