Phylogenetic stochastic mapping without matrix exponentiation

Abstract

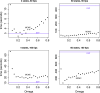
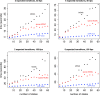
Phylogenetic stochastic mapping is a method for reconstructing the history of trait changes on a phylogenetic tree relating species/organism carrying the trait. State-of-the-art methods assume that the trait evolves according to a continuous-time Markov chain (CTMC) and works well for small state spaces. The computations slow down considerably for larger state spaces (e.g., space of codons), because current methodology relies on exponentiating CTMC infinitesimal rate matrices-an operation whose computational complexity grows as the size of the CTMC state space cubed. In this work, we introduce a new approach, based on a CTMC technique called uniformization, which does not use matrix exponentiation for phylogenetic stochastic mapping. Our method is based on a new Markov chain Monte Carlo (MCMC) algorithm that targets the distribution of trait histories conditional on the trait data observed at the tips of the tree. The computational complexity of our MCMC method grows as the size of the CTMC state space squared. Moreover, in contrast to competing matrix exponentiation methods, if the rate matrix is sparse, we can leverage this sparsity and increase the computational efficiency of our algorithm further. Using simulated data, we illustrate advantages of our MCMC algorithm and investigate how large the state space needs to be for our method to outperform matrix exponentiation approaches. We show that even on the moderately large state space of codons our MCMC method can be significantly faster than currently used matrix exponentiation methods.

Keywords: MCMC; codon models; data augmentation; evolution; uniformization.

FIG. 1.

An example of applying the two Markov kernels of our MCMC sampler to an augmented substitution history. The diamonds represent virtual transitions. (A) shows an initial augmented substitution history; (B) shows the substitution history after resampling states on the phylogeny conditional on tip node states and the transition points (both real and virtual); (C) shows the substitution history seen in (B) with no virtual jumps; and (D) shows the augmented substitution history after resampling virtual jumps conditional on the substitution history seen in (C). The transition from (A) to (B) shows the effect of the first Markov kernel, sampling from . The transition from (C) to (D) shows the effect of the second Markov kernel, sampling from .

FIG. 2.

State space effect. All four plots show the amount of time required to obtain 10,000 effective samples as a function of the size of the state space for two methods, matrix exponentiation in purple squares and our MCMC sampler in black circles. The two plots in the top row show results for a randomly generated tree with 50 tips. The two plots in the bottom row show results for a randomly generated tree with 100 tips. The two plots in the left column show results for a rate matrix that was scaled to produce two expected transitions while the two plots in the right column show results for a rate matrix that was scaled to produce six expected transitions.

FIG. 3.

Time to obtain 10,000 effective samples as a function of the dominating Poisson process rate, Ω. All four plots show results of our MCMC sampler in black. Timing results for the matrix exponentiation method are represented by a purple horizontal line because the matrix exponentiation result does not vary as a function of Ω. The two plots in the top row show results for a randomly generated tree with 50 tips. The two plots in the bottom row show results for a randomly generated tree with 100 tips. The rate matrix for the plots in the left column had four states. The rate matrix for the plots in the right column had 60 states.

FIG. 4.

Time to obtain 10,000 effective samples as a function of the size of the state space. All four plots show results for three different implementations, our MCMC sampler in black, a sparse version of our MCMC sampler in red, and a matrix exponentiation approach that only exponentiates the rate matrix once per branch in blue. The rate matrix is tridiagonal and scaled to produce two expected transitions per tree (in the left column) or six expected transitions per tree (in the right column). The two plots in the top row show results for a randomly generated tree with 50 tips. The two plots in the bottom row show results for a randomly generated tree with 100 tips. The dominating Poisson process rate, Ω, is 0.2.

FIG. 5.

Time to obtain 10,000 effective samples as a function of the dominating Poisson process rate, Ω, for the GY94 codon rate matrix. All four plots show results for three different implementations: our MCMC sampler in black, a sparse version of our MCMC sampler in red, and a matrix exponentiation approach in purple. The GY94 rate matrix was scaled to produce 2 expected transitions per tree (in the left column) or 6 expected transitions per tree (in the right column). The two plots in the top row show results for a randomly generated tree with 50 tips. The two plots in the bottom row show results for a randomly generated tree with 100 tips.