Computational modelling suggests good, bad and ugly roles of glycosaminoglycans in arterial wall mechanics and mechanobiology
- PMID: 24920112
- PMCID: PMC4208372
- DOI: 10.1098/rsif.2014.0397
Computational modelling suggests good, bad and ugly roles of glycosaminoglycans in arterial wall mechanics and mechanobiology
Abstract
The medial layer of large arteries contains aggregates of the glycosaminoglycan hyaluronan and the proteoglycan versican. It is increasingly thought that these aggregates play important mechanical and mechanobiological roles despite constituting only a small fraction of the normal arterial wall. In this paper, we offer a new hypothesis that normal aggregates of hyaluronan and versican pressurize the intralamellar spaces, and thereby put into tension the radial elastic fibres that connect the smooth muscle cells to the elastic laminae, which would facilitate mechanosensing. This hypothesis is supported by novel computational simulations using two complementary models, a mechanistically based finite-element mixture model and a phenomenologically motivated continuum hyperelastic model. That is, the simulations suggest that normal aggregates of glycosaminoglycans/proteoglycans within the arterial media may play equally important roles in supporting (i.e. a structural role) and sensing (i.e. an instructional role) mechanical loads. Additional simulations suggest further, however, that abnormal increases in these aggregates, either distributed or localized, may over-pressurize the intralamellar units. We submit that these situations could lead to compromised mechanosensing, anoikis and/or reduced structural integrity, each of which represent fundamental aspects of arterial pathologies seen, for example, in hypertension, ageing and thoracic aortic aneurysms and dissections.
Keywords: anoikis; hyaluronan; mechanosensing; stress analysis; versican.
© 2014 The Author(s) Published by the Royal Society. All rights reserved.
Figures
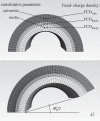
 , homeostatic (swollen homeostatic) configuration at a mean arterial pressure of 93 mmHg and in vivo axial stretch
, homeostatic (swollen homeostatic) configuration at a mean arterial pressure of 93 mmHg and in vivo axial stretch  (
( ). κp (
). κp ( ), loaded (swollen loaded) configurations at
), loaded (swollen loaded) configurations at  (
( ) and any pressure P, with representative values shown for P = 220 mmHg. κtf (
) and any pressure P, with representative values shown for P = 220 mmHg. κtf ( ), intact (swollen intact), traction-free configuration. κc (
), intact (swollen intact), traction-free configuration. κc ( ), radially cut (swollen radially cut), traction-free configuration. κn, natural (i.e. stress-free) configurations for individual constituents.
), radially cut (swollen radially cut), traction-free configuration. κn, natural (i.e. stress-free) configurations for individual constituents.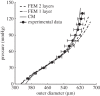
 . Note the good agreement between the two different modelling approaches. (b,d) Associated transmural distributions of circumferential (solid line) and axial (dashed line) Cauchy wall stress calculated using the continuum model for an axial stretch of
. Note the good agreement between the two different modelling approaches. (b,d) Associated transmural distributions of circumferential (solid line) and axial (dashed line) Cauchy wall stress calculated using the continuum model for an axial stretch of  (top) and
(top) and  (bottom) and an internal pressure of 93.3 mmHg. Also shown is the mean circumferential stress obtained via the classical Laplace relation (dotted-dashed line).
(bottom) and an internal pressure of 93.3 mmHg. Also shown is the mean circumferential stress obtained via the classical Laplace relation (dotted-dashed line).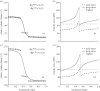
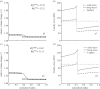
 . (b,d) Associated transmural distributions of circumferential (solid line) and axial (dashed line) Cauchy wall stress calculated using the continuum model for an axial stretch of
. (b,d) Associated transmural distributions of circumferential (solid line) and axial (dashed line) Cauchy wall stress calculated using the continuum model for an axial stretch of  (top) and
(top) and  (bottom) and an internal pressure of 93.3 mmHg. Also shown is the mean circumferential stress obtained via the classical Laplace relation (dotted-dashed line).
(bottom) and an internal pressure of 93.3 mmHg. Also shown is the mean circumferential stress obtained via the classical Laplace relation (dotted-dashed line).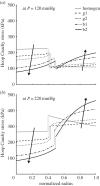
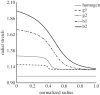

Similar articles
-
Local versus global mechanical effects of intramural swelling in carotid arteries.J Biomech Eng. 2015 Apr;137(4):041008. doi: 10.1115/1.4029303. Epub 2015 Feb 16. J Biomech Eng. 2015. PMID: 25474096 Free PMC article.
-
Biomechanical roles of medial pooling of glycosaminoglycans in thoracic aortic dissection.Biomech Model Mechanobiol. 2014 Jan;13(1):13-25. doi: 10.1007/s10237-013-0482-3. Epub 2013 Mar 15. Biomech Model Mechanobiol. 2014. PMID: 23494585 Free PMC article.
-
Finite element modelling of the common carotid artery in the elderly with physiological intimal thickening using layer-specific stress-released geometries and nonlinear elastic properties.Comput Methods Biomech Biomed Engin. 2016 Sep;19(12):1286-96. doi: 10.1080/10255842.2015.1128530. Epub 2015 Dec 29. Comput Methods Biomech Biomed Engin. 2016. PMID: 26710676
-
Glycosaminoglycans as key molecules in atherosclerosis: the role of versican and hyaluronan.Curr Med Chem. 2010;17(33):4018-26. doi: 10.2174/092986710793205354. Curr Med Chem. 2010. PMID: 20939824 Review.
-
Carotid atherosclerosis, arterial stiffness and stroke events.Adv Cardiol. 2007;44:173-186. doi: 10.1159/000096729. Adv Cardiol. 2007. PMID: 17075207 Review.
Cited by
-
Internal modulation of proteolysis in vascular extracellular matrix remodeling: role of ADAM metallopeptidase with thrombospondin type 1 motif 5 in the development of intracranial aneurysm rupture.Aging (Albany NY). 2021 May 2;13(9):12800-12816. doi: 10.18632/aging.202948. Epub 2021 May 2. Aging (Albany NY). 2021. PMID: 33934089 Free PMC article.
-
Glycosaminoglycans contribute to extracellular matrix fiber recruitment and arterial wall mechanics.Biomech Model Mechanobiol. 2017 Feb;16(1):213-225. doi: 10.1007/s10237-016-0811-4. Epub 2016 Aug 4. Biomech Model Mechanobiol. 2017. PMID: 27491312 Free PMC article.
-
Biomechanics of soft biological tissues and organs, mechanobiology, homeostasis and modelling.J R Soc Interface. 2025 Jan;22(222):20240361. doi: 10.1098/rsif.2024.0361. Epub 2025 Jan 29. J R Soc Interface. 2025. PMID: 39876788 Free PMC article. Review.
-
Simulating progressive intramural damage leading to aortic dissection using DeepONet: an operator-regression neural network.J R Soc Interface. 2022 Feb;19(187):20210670. doi: 10.1098/rsif.2021.0670. Epub 2022 Feb 9. J R Soc Interface. 2022. PMID: 35135299 Free PMC article.
-
Paradoxical aortic stiffening and subsequent cardiac dysfunction in Hutchinson-Gilford progeria syndrome.J R Soc Interface. 2020 May;17(166):20200066. doi: 10.1098/rsif.2020.0066. Epub 2020 May 27. J R Soc Interface. 2020. PMID: 32453981 Free PMC article.
References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

