Oedema-based model for diffuse low-grade gliomas: application to clinical cases under radiotherapy
- PMID: 24947764
- PMCID: PMC6496677
- DOI: 10.1111/cpr.12114
Oedema-based model for diffuse low-grade gliomas: application to clinical cases under radiotherapy
Abstract
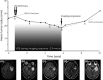
Objectives: Diffuse low-grade gliomas are characterized by slow growth. Despite appropriate treatment, they change inexorably into more aggressive forms, jeopardizing the patient's life. Optimizing treatments, for example with the use of mathematical modelling, could help to prevent tumour regrowth and anaplastic transformation. Here, we present a model of the effect of radiotherapy on such tumours. Our objective is to explain observed delay of tumour regrowth following radiotherapy and to predict its duration.
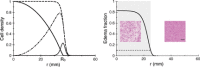
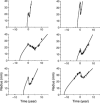
Materials and methods: We have used a migration-proliferation model complemented by an equation describing appearance and draining of oedema. The model has been applied to clinical data of tumour radius over time, for a population of 28 patients.
Results: We were able to show that draining of oedema accounts for regrowth delay after radiotherapy and have been able to fit the clinical data in a robust way. The model predicts strong correlation between high proliferation coefficient and low progression-free gain of lifetime, due to radiotherapy among the patients, in agreement with clinical studies. We argue that, with reasonable assumptions, it is possible to predict (precision ~20%) regrowth delay after radiotherapy and the gain of lifetime due to radiotherapy.
Conclusions: Our oedema-based model provides an early estimation of individual duration of tumour response to radiotherapy and thus, opens the door to the possibility of personalized medicine.
© 2014 John Wiley & Sons Ltd.
Conflict of interest statement
No potential conflicts of interest were disclosed.
Figures




Similar articles
-
Non-standard radiotherapy fractionations delay the time to malignant transformation of low-grade gliomas.PLoS One. 2017 Jun 1;12(6):e0178552. doi: 10.1371/journal.pone.0178552. eCollection 2017. PLoS One. 2017. PMID: 28570587 Free PMC article.
-
Predicting regrowth of low-grade gliomas after radiotherapy.PLoS Comput Biol. 2023 Mar 31;19(3):e1011002. doi: 10.1371/journal.pcbi.1011002. eCollection 2023 Mar. PLoS Comput Biol. 2023. PMID: 37000852 Free PMC article.
-
Simulating radiotherapy effect in high-grade glioma by using diffusive modeling and brain atlases.J Biomed Biotechnol. 2012;2012:715812. doi: 10.1155/2012/715812. Epub 2012 Oct 3. J Biomed Biotechnol. 2012. PMID: 23093856 Free PMC article.
-
Clinical features, mechanisms, and management of pseudoprogression in malignant gliomas.Lancet Oncol. 2008 May;9(5):453-61. doi: 10.1016/S1470-2045(08)70125-6. Lancet Oncol. 2008. PMID: 18452856 Review.
-
[Pattern of care of high-grade gliomas].Rev Prat. 2006 Oct 31;56(16):1779-86. Rev Prat. 2006. PMID: 17315503 Review. French.
Cited by
-
Biopsy location and tumor-associated macrophages in predicting malignant glioma recurrence using an in-silico model.NPJ Syst Biol Appl. 2025 Jan 8;11(1):3. doi: 10.1038/s41540-024-00478-7. NPJ Syst Biol Appl. 2025. PMID: 39779740 Free PMC article.
-
Computational design of improved standardized chemotherapy protocols for grade II oligodendrogliomas.PLoS Comput Biol. 2019 Jul 15;15(7):e1006778. doi: 10.1371/journal.pcbi.1006778. eCollection 2019 Jul. PLoS Comput Biol. 2019. PMID: 31306418 Free PMC article.
-
A mechanically coupled reaction-diffusion model that incorporates intra-tumoural heterogeneity to predict in vivo glioma growth.J R Soc Interface. 2017 Mar;14(128):20161010. doi: 10.1098/rsif.2016.1010. J R Soc Interface. 2017. PMID: 28330985 Free PMC article.
-
Non-standard radiotherapy fractionations delay the time to malignant transformation of low-grade gliomas.PLoS One. 2017 Jun 1;12(6):e0178552. doi: 10.1371/journal.pone.0178552. eCollection 2017. PLoS One. 2017. PMID: 28570587 Free PMC article.
-
Overcoming chemotherapy resistance in low-grade gliomas: A computational approach.PLoS Comput Biol. 2023 Nov 20;19(11):e1011208. doi: 10.1371/journal.pcbi.1011208. eCollection 2023 Nov. PLoS Comput Biol. 2023. PMID: 37983271 Free PMC article.
References
-
- Pallud J, Mandonnet E (2011) Quantitative approach of the natural course of diffuse low‐grade gliomas In: Hayat MA, ed. Tumors of the Central Nervous System, Vol. 2, pp. 163–172. Netherlands: Springer.
-
- Price SJ (2010) Advances in imaging low‐grade gliomas. Adv. Tech. Stand. Neurosurg. 35, 1–34. - PubMed
-
- Pallud J, Fontaine D, Duffau H, Mandonnet E, Sanai N, Taillandier L et al (2010) Natural history of incidental WHO grade II gliomas. Ann. Neurol. 68, 727–733. - PubMed
-
- Daumas‐Duport C, Meder JF, Monsaingeon V, Missir O, Aubin ML, Szikla G (1983) Cerebral gliomas: malignancy, limits and spatial configuration‐comparative data from serial stereotaxic biopsies and computed tomography (a preliminary study based on 50 cases). J. Neuroradiol. 10, 51–80. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

