In situ determination of alveolar septal strain, stress and effective Young's modulus: an experimental/computational approach

Abstract

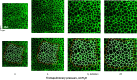
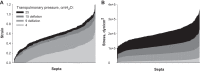
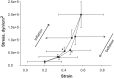
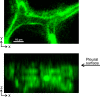
Alveolar septa, which have often been modeled as linear elements, may distend due to inflation-induced reduction in slack or increase in tissue stretch. The distended septum supports tissue elastic and interfacial forces. An effective Young's modulus, describing the inflation-induced relative displacement of septal end points, has not been determined in situ for lack of a means of determining the forces supported by septa in situ. Here we determine such forces indirectly according to Mead, Takishima, and Leith's classic lung mechanics analysis (J Appl Physiol 28: 596-608, 1970), which demonstrates that septal connections transmit the transpulmonary pressure, PTP, from the pleural surface to interior regions. We combine experimental septal strain determination and computational stress determination, according to Mead et al., to calculate effective Young's modulus. In the isolated, perfused rat lung, we label the perfusate with fluorescence to visualize the alveolar septa. At eight PTP values around a ventilation loop between 4 and 25 cmH2O, and upon total deflation, we image the same region by confocal microscopy. Within an analysis region, we measure septal lengths. Normalizing by unstressed lengths at total deflation, we calculate septal strains for all PTP > 0 cmH2O. For the static imaging conditions, we computationally model application of PTP to the boundary of the analysis region and solve for septal stresses by least squares fit of an overdetermined system. From group septal strain and stress values, we find effective septal Young's modulus to range from 1.2 × 10(5) dyn/cm(2) at low P(TP) to 1.4 × 10(6) dyn/cm(2) at high P(TP).

Keywords: alveolar septum; intact lung; modulus; strain; stress.

Fig. 1.

Forces acting on a section of in situ alveolar septum. Alveolar septal tissue (gray) is lined on each side by a thin liquid layer (white). The combined tissue/liquid structure is surrounded by air. At sections through the septum (all 4 edges), tissue stress acts throughout the tissue and surface tension at the air-liquid interface.

Fig. 2.

Septal element model. Top: confocal microscopy images of fluorescently labeled vasculature in subpleural alveoli of isolated, perfused rat lung, at 4 transpulmonary pressure, P_TP, values, on deflation. At P_TP of 4 cmH₂O, subpleural depth is 24 μm. Bottom: same images with overlay of alveolar element model. Alveolar septa are represented by linear elements: red on periphery of region to be analyzed, white in interior. Dashed elements indicate cross-bridge structures that arch over the tops of alveoli.

Fig. 3.

Subpleural septal morphology. Alveoli imaged at P_TP of 4 cmH₂O. Top images show x–y plane of analysis that is parallel to and 22 μm below the pleural surface. Bottom images show x–z sections, with the pleural surface at their tops, constructed from z-stacks of x–y optical sections. The x–z sections intersect the x–y sections along the long axes of the white dotted ovals in the x–y sections. A: subpleural septa are typically oriented perpendicular to the pleural surface. Red arrows show capillary thickness, t_C, of 4.2 μm. B: what look like cross bridges across some alveoli, as viewed in the x–y plane, are arch structures across the tops of the alveoli, as viewed in the x–z plane.

Fig. 4.

Modeling P_TP application to the periphery of the analyzed interior lung region. Heavy line indicates periphery of analyzed lung region. A: according to Mead et al. (12), alveolar septa connecting to the outside of an internal lung region and supporting forces F_O transmit P_TP to the interior lung region. Septa within the interior region apply forces F_I to the periphery of the region. B: as forces F_O transmit P_TP to the interior region, we replace them, in our analysis, with application of P_TP directly to the periphery of the interior region. C: for each peripheral element in our linear element model, we calculate the force F_PTP due to pressure acting on the element and apply half of the force at each end point of the element. D: forces acting on peripheral element enclosed by dotted oval in A. Upper left end point is loaded by F_O and also F_P1 from the connecting peripheral element to left. Lower right end point is loaded by F_I and also F_P2 from the connecting peripheral element to right. E: forces acting on peripheral element enclosed by dotted oval in C. Force F_O at upper left end point of the element in D has been replaced by 4 forces due to P_TP, split between both end points (Ei). The 2 forces due to P_TP at each end point may be summed (Eii). Replacement of F_O at 1 end point of the analyzed peripheral element by F_PTP split between its 2 end points reduces loading of the analyzed peripheral element in E compared with that in D.

Fig. 5.

Septal strain and stress. Sorted strain (A) and stress (B) data at 4 P_TP values on deflation. Data presented for n = 322 septa. Peripheral septa, cross bridges, and septa with an unstressed length L₀ < 20 μm are omitted.

Fig. 6.

Septal strain and stress values in an imaged/modeled lung region at P_TP of 9 cmH₂O on deflation. Peripheral septa, cross bridges, and septa with an unstressed length L₀ < 20 μm are omitted. *Large alveoli lacking cross bridges.

Fig. 7.

Septal stress-strain relation. Median stress vs. median strain at 8 P_TP around the ventilation loop, for n = 322 septa. Peripheral septa, cross bridges, and septa with an unstressed length L₀ < 20 μm are omitted. Strain and stress both differ significantly (P < 0.05) between the end points of each segment of the stress-strain loop, excepting that there is no difference in strain between P_TP of 25 cmH₂O and 15 cmH₂O on deflation. At P_TP of 9 cmH₂O (*), strain (P < 0.01) and stress (P < 0.01) are greater on deflation than on inflation. At P_TP of 15 cmH₂O (#), strain (P < 0.01) is greater on deflation than on inflation.

Fig. A1.

A subpleural septum imaged in a perfused (12 ml/min) lung without use of a coverslip at P_TP of 15 cmH₂O. Top: x–y section through septum. Bottom: x–z section shows linear border at top of septum where septum intersects with pleural surface. Fluorescence is dye calcein AM loaded into alveolar epithelium.

Fig. A2.

Stresses determined in x–y analysis plane are principal stresses. Left: schematic of planar subpleural septum and its linear junction with the pleural surface. Although subpleural septa typically meet the pleural surface at an angle, θ, of 90°, analysis (see appendix text) is not restricted to any particular θ value. Right: detail of portion of subpleural septum enclosed by dotted line on left. Normal (σ) and shear (τ) stresses act on each edge of the section, with normal stress σ_zz on the top edge attributable to application of the P_TP to the pleural surface. Because the top edge cannot support a shear stress (see text), all shear stresses are zero and normal stresses σ_xx and σ_zz are principal stresses. The x–y plane of our stress-strain analysis is aligned the axis of the principal stress σ_xx.