Quantifying 'causality' in complex systems: understanding transfer entropy
- PMID: 24955766
- PMCID: PMC4067287
- DOI: 10.1371/journal.pone.0099462
Quantifying 'causality' in complex systems: understanding transfer entropy
Abstract
'Causal' direction is of great importance when dealing with complex systems. Often big volumes of data in the form of time series are available and it is important to develop methods that can inform about possible causal connections between the different observables. Here we investigate the ability of the Transfer Entropy measure to identify causal relations embedded in emergent coherent correlations. We do this by firstly applying Transfer Entropy to an amended Ising model. In addition we use a simple Random Transition model to test the reliability of Transfer Entropy as a measure of 'causal' direction in the presence of stochastic fluctuations. In particular we systematically study the effect of the finite size of data sets.
Conflict of interest statement
Figures
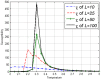
 .
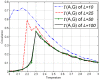
.
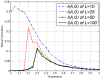

 .
.
 .
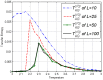
.
 .
.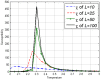
 .
.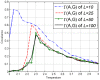
 , similar to Figure (2) of the Ising model.
, similar to Figure (2) of the Ising model.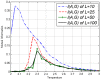
 at time lag
at time lag  is indicated. Very different from result on Ising model in Figure 4.
is indicated. Very different from result on Ising model in Figure 4.
 which is very different from Figure (5).
which is very different from Figure (5).
 , similar to Ising model results in Figure (6).
, similar to Ising model results in Figure (6).
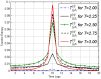
 . Figure highlights time lag detection.
. Figure highlights time lag detection.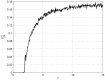
 due to distance (separation) in space where
due to distance (separation) in space where  is closer to
is closer to  than
than  . The nearest neighbour effect is observed.
. The nearest neighbour effect is observed.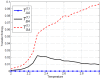
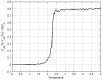
 due to implanted ‘causal’ lag. The effect of separation in space is no longer visible.
due to implanted ‘causal’ lag. The effect of separation in space is no longer visible.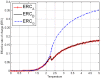
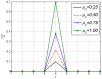
 is monotonically increasing with respect to
is monotonically increasing with respect to  .
.  is affected by
is affected by  . Figure illustrates how the internal dynamics of
. Figure illustrates how the internal dynamics of  influences
influences  when
when  is the target variable. Transfer Entropy changes even though external influence
is the target variable. Transfer Entropy changes even though external influence  is constant.
is constant.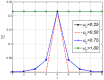
 ,
,  does not effect
does not effect  and values remain constant. For
and values remain constant. For  at
at  , Transfer Entropy is affected by
, Transfer Entropy is affected by  .
.  and
and  coincides. Figure shows how the internal dynamics of
coincides. Figure shows how the internal dynamics of  influences
influences  when
when  is the source variable.
is the source variable.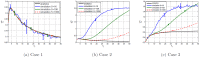
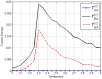
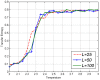
 are uniformly distributed. Analytical values obtained from substituting respective
are uniformly distributed. Analytical values obtained from substituting respective  values in equation (17). Simulated values are acquired using equation (5) on simulated data of varying sample size
values in equation (17). Simulated values are acquired using equation (5) on simulated data of varying sample size  (length of time series) where
(length of time series) where  . Error bars are displaying two standard deviation values above and two standard deviation below (some bars are very small, it can barely be seen). The aim is primarily to display how choosing
. Error bars are displaying two standard deviation values above and two standard deviation below (some bars are very small, it can barely be seen). The aim is primarily to display how choosing  has to be made according to length,
has to be made according to length,  , of available time series. For large
, of available time series. For large  the error bar becomes smaller than the width of the curve.
the error bar becomes smaller than the width of the curve.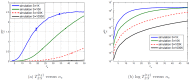
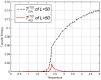
 . Error bars in the first figure are displaying two standard deviation values above and two standard deviation below. For large
. Error bars in the first figure are displaying two standard deviation values above and two standard deviation below. For large  the error bar becomes smaller than the width of the curve. In order to use the null model as surrogates,
the error bar becomes smaller than the width of the curve. In order to use the null model as surrogates,  still has to be chosen in accordance to
still has to be chosen in accordance to  .
.References
-
- Bak P (1996) How Nature Works: The Science of Self Organized Criticality. New York: Springer-Verlag.
-
- Christensen K, Moloney RN (2005) Complexity and Criticality. London: Imperial College Press.
-
- Jensen HJ (1998) Self Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems. Cambridge: Cambridge University Press.
-
- Pruessner G (2012) Self-Organised Criticality: Theory, Models and Characterisation. Cambridge: Cambridge University Press.
-
- Jensen HJ (2009) Probability and statistics in complex systems, introduction to. In: Encyclopedia of Complexity and Systems Science. pp. 7024–7025.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

