Assessing dynamic spectral causality by lagged adaptive directed transfer function and instantaneous effect factor

Abstract

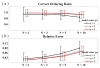
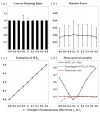
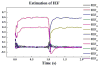
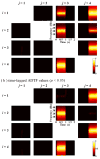
It is of significance to assess the dynamic spectral causality among physiological signals. Several practical estimators adapted from spectral Granger causality have been exploited to track dynamic causality based on the framework of time-varying multivariate autoregressive (tvMVAR) models. The nonzero covariance of the model's residuals has been used to describe the instantaneous effect phenomenon in some causality estimators. However, for the situations with Gaussian residuals in some autoregressive models, it is challenging to distinguish the directed instantaneous causality if the sufficient prior information about the "causal ordering" is missing. Here, we propose a new algorithm to assess the time-varying causal ordering of tvMVAR model under the assumption that the signals follow the same acyclic causal ordering for all time lags and to estimate the instantaneous effect factor (IEF) value in order to track the dynamic directed instantaneous connectivity. The time-lagged adaptive directed transfer function (ADTF) is also estimated to assess the lagged causality after removing the instantaneous effect. In this study, we first investigated the performance of the causal-ordering estimation algorithm and the accuracy of IEF value. Then, we presented the results of IEF and time-lagged ADTF method by comparing with the conventional ADTF method through simulations of various propagation models. Statistical analysis results suggest that the new algorithm could accurately estimate the causal ordering and give a good estimation of the IEF values in the Gaussian residual conditions. Meanwhile, the time-lagged ADTF approach is also more accurate in estimating the time-lagged dynamic interactions in a complex nervous system after extracting the instantaneous effect. In addition to the simulation studies, we applied the proposed method to estimate the dynamic spectral causality on real visual evoked potential (VEP) data in a human subject. Its usefulness in time-variant spectral causality assessment was demonstrated through the mutual causality investigation of brain activity during the VEP experiments.

Fig. 1

Graphical illustration of the model 3. (a) During the first half of the time (0–1s), node 3 is the primary source. It propagates to node 4 in the time-lagged pattern, propagates to node 1 in the zero-lagged pattern, and propagates to node 2 in the fused pattern. (b) During the later portion of the time (1–2s), node 4 becomes the main source and causes the other nodes in different propagation patterns. a_ij is the time dependent amplitude of the connection between ith and jth node, τ_ij denotes the constant delay in the propagation from the jth to the ith node, and IEF_ij is the instantaneous connectivity strength.

Fig. 2

The plots show the (a) correct ordering ratio and (b) relative error with different number of variables (N) and model orders (p) from the causal ordering estimation algorithm in simulated model 1.

Fig. 3

The results of the simulated model 2: The plot of COR (a), RE (b) and the estimation of IEF₂₁ (c) vs. instantaneous connectivity strength factor α. (d) The plot of means for the significant (p < 0.05) causality values (x₁ -> x₂) within the frequency band of 9–14 Hz. Black, gray, and red colors represent the ADTF values, time-lagged ADTF values and theoretical values, respectively.

Fig. 4

The estimation of the time-varying IEF values between all signals in model 3, averaged from 1000 trials.

Fig. 5

The time-frequency distribution of the significant (p < 0.05) causality values between all the signals in simulated model 3. (a) ADTF method results, and (b) time-lagged ADTF method results.

Fig. 6

(a) The averaged VEP signals of the nine electrodes (P1, Pz, P2, PO3, POz, PO4, O1, Oz and O2) in lower-left condition. (b) The main structure of IEF and the plots of IEF values from PO4 and O2 to the other signals. (c) The main connectivity structure and the time-frequency distribution of the significant (p < 0.01) causality values by the ADTF method. (d) The main connectivity structure and the time-frequency distribution of the significant (p < 0.01) causality values by the time-lagged ADTF method. The color of the arrows codes the averaged strength of the absolute connectivity values over the time and the interesting frequency band (1–30Hz).