Determining enzyme kinetics for systems biology with nuclear magnetic resonance spectroscopy
- PMID: 24957764
- PMCID: PMC3901242
- DOI: 10.3390/metabo2040818
Determining enzyme kinetics for systems biology with nuclear magnetic resonance spectroscopy
Abstract
Enzyme kinetics for systems biology should ideally yield information about the enzyme's activity under in vivo conditions, including such reaction features as substrate cooperativity, reversibility and allostery, and be applicable to enzymatic reactions with multiple substrates. A large body of enzyme-kinetic data in the literature is based on the uni-substrate Michaelis-Menten equation, which makes unnatural assumptions about enzymatic reactions (e.g., irreversibility), and its application in systems biology models is therefore limited. To overcome this limitation, we have utilised NMR time-course data in a combined theoretical and experimental approach to parameterize the generic reversible Hill equation, which is capable of describing enzymatic reactions in terms of all the properties mentioned above and has fewer parameters than detailed mechanistic kinetic equations; these parameters are moreover defined operationally. Traditionally, enzyme kinetic data have been obtained from initial-rate studies, often using assays coupled to NAD(P)H-producing or NAD(P)H-consuming reactions. However, these assays are very labour-intensive, especially for detailed characterisation of multi-substrate reactions. We here present a cost-effective and relatively rapid method for obtaining enzyme-kinetic parameters from metabolite time-course data generated using NMR spectroscopy. The method requires fewer runs than traditional initial-rate studies and yields more information per experiment, as whole time-courses are analyzed and used for parameter fitting. Additionally, this approach allows real-time simultaneous quantification of all metabolites present in the assay system (including products and allosteric modifiers), which demonstrates the superiority of NMR over traditional spectrophotometric coupled enzyme assays. The methodology presented is applied to the elucidation of kinetic parameters for two coupled glycolytic enzymes from Escherichia coli (phosphoglucose isomerase and phosphofructokinase). 31P-NMR time-course data were collected by incubating cell extracts with substrates, products and modifiers at different initial concentrations. NMR kinetic data were subsequently processed using a custom software module written in the Python programming language, and globally fitted to appropriately modified Hill equations.
Figures


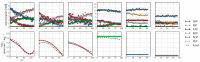
 , ATP
, ATP  , FBP
, FBP  , ADP
, ADP  , PEP
, PEP  ) are fitted with splines (G6P
) are fitted with splines (G6P  , F6P
, F6P  , ATP
, ATP  , FBP
, FBP  , ADP
, ADP  , PEP
, PEP  ). Inhibitor assays containing PEP are shown in the last two blocks. Note that with the exception of the second-last assay, F6P concentrations are inferred from equilibrium with G6P via PGI. Bottom row: Respective rates derived from spline-fitted NMR data. Dual colour lines indicate an average of two respective rates. For comparison, the rate calculated by the irreversible Hill equation (---, Table 1: PFK) at the specific substrate, product and effector concentrations is shown. The Hill equation parameters were the same throughout and obtained from a global fit of all the time courses shown. Rates are normalised to total protein. Raw NMR FID data, as well as NMR peak integrals and spline data, are included as supplementary material.
). Inhibitor assays containing PEP are shown in the last two blocks. Note that with the exception of the second-last assay, F6P concentrations are inferred from equilibrium with G6P via PGI. Bottom row: Respective rates derived from spline-fitted NMR data. Dual colour lines indicate an average of two respective rates. For comparison, the rate calculated by the irreversible Hill equation (---, Table 1: PFK) at the specific substrate, product and effector concentrations is shown. The Hill equation parameters were the same throughout and obtained from a global fit of all the time courses shown. Rates are normalised to total protein. Raw NMR FID data, as well as NMR peak integrals and spline data, are included as supplementary material.
 ), arrows indicate both the metabolite concentrations and the direction of reaction as each time course progresses towards equilibrium (→→→). The rate was normalised to total protein concentration. Substrate and product concentration axes are in logarithmic scale. R2= 0.99.
), arrows indicate both the metabolite concentrations and the direction of reaction as each time course progresses towards equilibrium (→→→). The rate was normalised to total protein concentration. Substrate and product concentration axes are in logarithmic scale. R2= 0.99.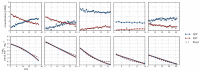
 ) and product F6P (
) and product F6P ( ) and monitoring reaction progress using 31P NMR with a 90° pulse angle and 1 s repetition time (1.0 s acquisition, 0.0 s relaxation) with 80 transients per FID. Other parameters are as described in Section 3.3. Progress curves derived from NMR peak integrals were fitted with splines (G6P
) and monitoring reaction progress using 31P NMR with a 90° pulse angle and 1 s repetition time (1.0 s acquisition, 0.0 s relaxation) with 80 transients per FID. Other parameters are as described in Section 3.3. Progress curves derived from NMR peak integrals were fitted with splines (G6P  , F6P
, F6P  ). Bottom row: The respective averaged rates of the fitted splines are plotted (dual colours indicate average of two respective rates) with the rate of the fitted kinetic equation included (---, Table 1: PGI). Rates were normalised to total protein content. Raw NMR FID data, as well as NMR peak integrals and spline data, are included as supplementary material.
). Bottom row: The respective averaged rates of the fitted splines are plotted (dual colours indicate average of two respective rates) with the rate of the fitted kinetic equation included (---, Table 1: PGI). Rates were normalised to total protein content. Raw NMR FID data, as well as NMR peak integrals and spline data, are included as supplementary material.

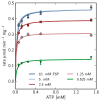
 ), 5mM (
), 5mM ( ), 2.5mM (
), 2.5mM ( ), 1.25mM (
), 1.25mM ( ), 0.625 mM (
), 0.625 mM ( ).
).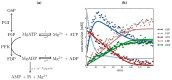
 , F6P
, F6P  , ATP
, ATP  , FBP
, FBP  , ADP
, ADP  ) compared with experimental time course data (G6P
) compared with experimental time course data (G6P  , F6P
, F6P  ., ATP
., ATP  , FBP
, FBP  , ADP
, ADP  ). The time course started with only F6P and ATP present as substrates. Note: for parameter fitting, F6P was assumed to be in equilibrium with G6P via the PGI reaction, and as such no quantified F6P data are included in this figure, except for an initial concentration. AMP and orthophosphate are not shown.
). The time course started with only F6P and ATP present as substrates. Note: for parameter fitting, F6P was assumed to be in equilibrium with G6P via the PGI reaction, and as such no quantified F6P data are included in this figure, except for an initial concentration. AMP and orthophosphate are not shown.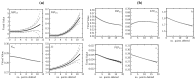
Similar articles
-
Enzyme dynamics from NMR spectroscopy.Acc Chem Res. 2015 Feb 17;48(2):457-65. doi: 10.1021/ar500340a. Epub 2015 Jan 9. Acc Chem Res. 2015. PMID: 25574774 Free PMC article. Review.
-
Michaelis-Menten equation for degradation of insoluble substrate.Math Biosci. 2018 Feb;296:93-97. doi: 10.1016/j.mbs.2017.11.011. Epub 2018 Jan 9. Math Biosci. 2018. PMID: 29197509
-
Evaluation of rate law approximations in bottom-up kinetic models of metabolism.BMC Syst Biol. 2016 Jun 6;10(1):40. doi: 10.1186/s12918-016-0283-2. BMC Syst Biol. 2016. PMID: 27266508 Free PMC article.
-
ICEKAT: an interactive online tool for calculating initial rates from continuous enzyme kinetic traces.BMC Bioinformatics. 2020 May 14;21(1):186. doi: 10.1186/s12859-020-3513-y. BMC Bioinformatics. 2020. PMID: 32410570 Free PMC article.
-
Modelling atypical CYP3A4 kinetics: principles and pragmatism.Arch Biochem Biophys. 2005 Jan 15;433(2):351-60. doi: 10.1016/j.abb.2004.09.010. Arch Biochem Biophys. 2005. PMID: 15581591 Review.
Cited by
-
Analysis of phosphofructokinase-1 activity as affected by pH and ATP concentration.Sci Rep. 2024 Sep 11;14(1):21192. doi: 10.1038/s41598-024-72028-4. Sci Rep. 2024. PMID: 39261563 Free PMC article.
-
Bottom-up parameterization of enzyme rate constants: Reconciling inconsistent data.Metab Eng Commun. 2024 Apr 23;18:e00234. doi: 10.1016/j.mec.2024.e00234. eCollection 2024 Jun. Metab Eng Commun. 2024. PMID: 38711578 Free PMC article.
-
Kinetic modelling: an integrated approach to analyze enzyme activity assays.Plant Methods. 2017 Aug 25;13:69. doi: 10.1186/s13007-017-0218-y. eCollection 2017. Plant Methods. 2017. PMID: 28855956 Free PMC article.
-
Real-time monitoring of the sialic acid biosynthesis pathway by NMR.Chem Sci. 2023 Feb 21;14(13):3482-3492. doi: 10.1039/d2sc06986e. eCollection 2023 Mar 29. Chem Sci. 2023. PMID: 37006695 Free PMC article.
-
The best models of metabolism.Wiley Interdiscip Rev Syst Biol Med. 2017 Nov;9(6):10.1002/wsbm.1391. doi: 10.1002/wsbm.1391. Epub 2017 May 19. Wiley Interdiscip Rev Syst Biol Med. 2017. PMID: 28544810 Free PMC article. Review.
References
-
- Teusink B., Passarge J., Reijenga C., Esgalhado E., van der Weijden C., Schepper M., Walsh M., Bakker B., van Dam K., Westerhoff H., et al. Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur. J. Biochem. 2000;267:5313–5329. doi: 10.1046/j.1432-1327.2000.01527.x. - DOI - PubMed
LinkOut - more resources
Full Text Sources

