Cycling empirical antibiotic therapy in hospitals: meta-analysis and models

Abstract

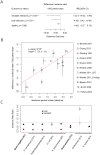
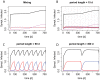
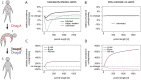
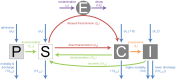
The rise of resistance together with the shortage of new broad-spectrum antibiotics underlines the urgency of optimizing the use of available drugs to minimize disease burden. Theoretical studies suggest that coordinating empirical usage of antibiotics in a hospital ward can contain the spread of resistance. However, theoretical and clinical studies came to different conclusions regarding the usefulness of rotating first-line therapy (cycling). Here, we performed a quantitative pathogen-specific meta-analysis of clinical studies comparing cycling to standard practice. We searched PubMed and Google Scholar and identified 46 clinical studies addressing the effect of cycling on nosocomial infections, of which 11 met our selection criteria. We employed a method for multivariate meta-analysis using incidence rates as endpoints and find that cycling reduced the incidence rate/1000 patient days of both total infections by 4.95 [9.43-0.48] and resistant infections by 7.2 [14.00-0.44]. This positive effect was observed in most pathogens despite a large variance between individual species. Our findings remain robust in uni- and multivariate metaregressions. We used theoretical models that reflect various infections and hospital settings to compare cycling to random assignment to different drugs (mixing). We make the realistic assumption that therapy is changed when first line treatment is ineffective, which we call "adjustable cycling/mixing". In concordance with earlier theoretical studies, we find that in strict regimens, cycling is detrimental. However, in adjustable regimens single resistance is suppressed and cycling is successful in most settings. Both a meta-regression and our theoretical model indicate that "adjustable cycling" is especially useful to suppress emergence of multiple resistance. While our model predicts that cycling periods of one month perform well, we expect that too long cycling periods are detrimental. Our results suggest that "adjustable cycling" suppresses multiple resistance and warrants further investigations that allow comparing various diseases and hospital settings.

Figure 1. Effect of clinical cycling vs. baseline period.

A) This figure shows the effect of clinical cycling on total incidence rate, weighted incidence rate of resistance, and mortality as estimated by a multivariate random-effects model. B) Performance of clinical cycling and pre-existing resistance. On the x-axis, the average number of resistances per isolate during the baseline period against antibiotics used in the clinical cycling regimen are given. On the y-axis, the success of clinical cycling as measured in the difference of total isolates per 1000 patient days is given. The error bars indicate the standard deviation for each study. The p-value as well as the slope of the regression line (red line) with 95% confidence interval of the regression is given in the figure. One study was omitted because of insufficient data. C) Pathogen-specific meta-analysis. Our outcome measures were the total number of isolates (black) and the weighted prevalence of resistance to the scheduled antibiotics (red). The number of studies giving data on the respective pathogen group is given in brackets (black = total number, red = resistant). Due to the sparsity of the data for individual pathogens, we used the Mantel-Haenszel method. Empty symbols indicate pathogen groups for which the omission of one single study changed the relative benefit of clinical cycling (e.g. clinical cycling was beneficial when all studies were considered, but the omission of one of these studies led to a detrimental outcome or vice versa).

Figure 2. Dynamics during “adjustable mixing” and “adjustable cycling” periods of different length.

The prevalence of symptomatically infected patients by strain genotype during deterministic realizations of scenario ii) (single-resistance among incoming patients) are shown. Red indicates resistance to drug A, blue indicates resistance to drug B, purple resistance to both drugs, and black the overall prevalence. Graph A) shows the dynamics during mixing, B)–D) during cycling with increasing period length. The grey vertical lines indicate a period change.

Figure 3. Cycling is successful when treatment is adjusted.

The schematic on the left illustrates treatment adjustment upon progression. A patient colonized (C) with an A-resistant pathogen as indicated by red circles and receiving drug A progresses to symptomatic disease (I) because the current drug is ineffective. Upon progression, the therapy under which the patient deteriorated is switched to drug B. This drug is effectively clearing the infection and the patient becomes susceptible (S) for new colonization. The left panel (A, C) shows a scenario where treatment is adjusted upon progression, the right panel (B, D) shows the same parameter without treatment adjustment. We modeled the scenario without treatment adjustment by setting the progression rate to zero, the treatment frequencies for colonized patients were adjusted to correspond to the overall treatment frequencies in our standard settings. The x-axis gives the period length, the y-axis the prevalence of single-resistant carriers relative to Mixing. The upper panel (A, B) shows the prevalence of colonized (green), symptomatically infected (black) and symptomatic patients who are inappropriately treated (grey). The lower panel (C, D) shows the genotype composition depending on the period length: red indicates resistance to A, blue resistance to B, and purple resistance to both drugs. The dotted black line indicates no difference in prevalence.

Figure 4. Compartmental model for single strain.

Explanations of the parameters, their standard values, the range over which we varied these parameters, as well as references are given in table S6. The compartments are: P = protected patients; S = susceptible patients; C = colonized patients; I = infected patients; E = environment. The color coded arrows indicate: violet = environmental contamination & decay; blue = admission & mortality/discharge; green = decolonization & recovery (this does not necessarily indicate full clearance of the pathogen from all body compartments, rather, it describes that the bacterial population has decreased sufficiently to allow a new strain to take over); orange = progression; red = transmission.

Figure 5. Treatment algorithm.

The superscript denotes the treatment status. Colonized patients are assigned with frequencies f _p and f _p,AB to treatment for other causes than symptomatic infections with the organism under consideration. If they progress to symptomatic disease and were previously treated with a single drug, this drug is then switched, while patients on both drugs remain on their treatment. Infected patients are assigned to treatments according to the current treatment strategy (mixing or cycling) immediately upon entering the ward.