Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Jun 30;22(13):15982-91.
doi: 10.1364/OE.22.015982.

Localization events-based sample drift correction for localization microscopy with redundant cross-correlation algorithm

Yina Wang, Joerg Schnitzbauer, Zhe Hu, Xueming Li, Yifan Cheng, Zhen-Li Huang, Bo Huang

Localization events-based sample drift correction for localization microscopy with redundant cross-correlation algorithm

Yina Wang et al. Opt Express. .

Abstract

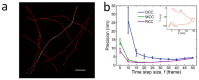
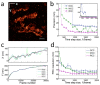
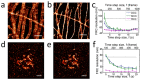
Highly accurate sample drift correction is essential in super-resolution localization microscopy to guarantee a high spatial resolution, especially when the technique is used to visualize small cell organelle. Here we present a localization events-based drift correction method using a redundant cross-correlation algorithm originally developed to correct beam-induced motion in cryo-electron microscopy. With simulated, synthesized as well as experimental data, we have demonstrated its superior precision compared to previously published localization events-based drift correction methods. The major advantage of this method is the robustness when the number of localization events is low, either because a short correction time step is required or because the imaged structure is small and sparse. This method has allowed us to improve the effective resolution when imaging Golgi apparatus in mammalian cells.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
The effect of correlation time-step size, f, on the cross-correlation map. (a) A super-resolution image of microtubules that contains severe sample drift. The image is spatially binned into a 2D histogram with a bin size of 30 nm. Scale bar: 1 μm. (b) One time segment with f = 1000 frames. (c) The cross-correlation function between the first and the last segments with f = 1000 frames. The white cross shows the auto-correlation peak of the first image. The arrow points out the direction and the amount of the drift between these two intervals. (d) The cross-correlation function between the first and the last segments with f = 100 frames. Note that the SNR in the map is greatly decreased.
Fig. 2
Fig. 2
The drift estimation precision of the direct, mean and redundant cross-correlation methods in analysing simulated super-resolution images. (a) Simulated perfect super-resolution image. Scale bar: 5 μm. (b) The influence of correlation time step size on drift measurement precision. The inset shows the amount of drift adding to the data sets. Each date point was averaged from five independent measurements. The error bars indicate standard deviations.
Fig. 3
Fig. 3
Drift correction performance of the direct, mean and redundant cross-correlation methods in analysing synthesized experimental images. (a) “Ground truth” Golgi super-resolution image. Scale bar: 1 μm. (b) The dependence of the drift measurement precision on correlation time step sizes. (c) The measured and real drift trajectory with the time step size, f = 1000 frames. (d) The dependence FRC resolution after drift correction on the correlation time step size. The black dashed line indicates the resolution of the “ground truth” image in (a).
Fig. 4
Fig. 4
The drift correction performance of the three methods in analysing experimental images containing microtubule (a-c) and Golgi (d-f) structures, showing the original, motion-blurred super-resolution images (a, d) and those corrected for sample drift by RCC (b, e). The independence of the FRC resolution (after drift correction) on the time step size is shown in (c) for the microtubule data set and (f) for the Golgi data set, respectively. The black dashed lines indicate the FRC resolution before drift correction. Scale bars: 1 μm (a,b) and 2 μm (d, e).
See this image and copyright information in PMC

References

    1. Betzig E., Patterson G. H., Sougrat R., Lindwasser O. W., Olenych S., Bonifacino J. S., Davidson M. W., Lippincott-Schwartz J., Hess H. F., “Imaging intracellular fluorescent proteins at nanometer resolution,” Science 313(5793), 1642–1645 (2006).10.1126/science.1127344 - DOI - PubMed
    1. Hess S. T., Girirajan T. P. K., Mason M. D., “Ultra-high resolution imaging by fluorescence photoactivation localization microscopy,” Biophys. J. 91(11), 4258–4272 (2006).10.1529/biophysj.106.091116 - DOI - PMC - PubMed
    1. Rust M. J., Bates M., Zhuang X. W., “Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM),” Nat. Methods 3(10), 793–796 (2006).10.1038/nmeth929 - DOI - PMC - PubMed
    1. Egner A., Geisler C., von Middendorff C., Bock H., Wenzel D., Medda R., Andresen M., Stiel A. C., Jakobs S., Eggeling C., Schönle A., Hell S. W., “Fluorescence nanoscopy in whole cells by asynchronous localization of photoswitching emitters,” Biophys. J. 93(9), 3285–3290 (2007).10.1529/biophysj.107.112201 - DOI - PMC - PubMed
    1. Lew M. D., Lee S. F., Ptacin J. L., Lee M. K., Twieg R. J., Shapiro L., Moerner W. E., “Three-dimensional superresolution colocalization of intracellular protein superstructures and the cell surface in live Caulobacter crescentus,” Proc. Natl. Acad. Sci. U.S.A. 108(46), E1102–E1110 (2011).10.1073/pnas.1114444108 - DOI - PMC - PubMed

Publication types