The optimal shape of elastomer mushroom-like fibers for high and robust adhesion

Abstract

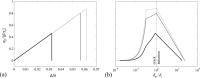
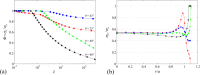
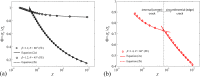
Over the last decade, significant effort has been put into mimicking the ability of the gecko lizard to strongly and reversibly cling to surfaces, by using synthetic structures. Among these structures, mushroom-like elastomer fiber arrays have demonstrated promising performance on smooth surfaces matching the adhesive strengths obtained with the natural gecko foot-pads. It is possible to improve the already impressive adhesive performance of mushroom-like fibers provided that the underlying adhesion mechanism is understood. Here, the adhesion mechanism of bio-inspired mushroom-like fibers is investigated by implementing the Dugdale-Barenblatt cohesive zone model into finite elements simulations. It is found that the magnitude of pull-off stress depends on the edge angle θ and the ratio of the tip radius to the stalk radius β of the mushroom-like fiber. Pull-off stress is also found to depend on a dimensionless parameter χ, the ratio of the fiber radius to a length-scale related to the dominance of adhesive stress. As an estimate, the optimal parameters are found to be β = 1.1 and θ = 45°. Further, the location of crack initiation is found to depend on χ for given β and θ. An analytical model for pull-off stress, which depends on the location of crack initiation as well as on θ and β, is proposed and found to agree with the simulation results. Results obtained in this work provide a geometrical guideline for designing robust bio-inspired dry fibrillar adhesives.

Keywords: adhesion; gecko; mushroom-like fibers.

Figure 1

Scanning electron microscope image of polyurethane mushroom-like fibers with 4 µm stalk radius, 8 µm tip radius, and 20 µm height.

Figure 2

Two-dimensional axial symmetry model for a mushroom-like fiber. The tip (top surface) is fixed in radial direction to simulate full-friction contact. DB cohesive zone model is implemented at the tip of the fiber in FE simulations.

Figure 3

Average tensile stress at the tip of the fiber (a) as a function of normalized far field displacement Δ/h, and (b) as a function of normalized maximum interfacial separation δ_m/δ_c for β = 1.2 and θ = 25° (dark gray), θ = 45° (light gray), and θ = 75° (black). Here, δ_c = 1 nm (χ = 6). Peaks in each plot for specific θ coincide and correspond to normalized pull-off stress Φ. Tensile load drops immediately after the maximum interfacial separation reaches the critical separation indicating that the contact is unstable following crack initiation. The discontinuity at δ_m/δ_c ≈ 0.1 prior to crack initiation in (b) marks the instant when a cohesive zone starts to form.

Figure 4

Normalized pull-off stress Φ contour plots for χ = 5 (top left), χ = 10 (top right), χ = 20 (bottom left), and χ = 40 (bottom right) as a function of β and θ. The peak Φ for each case lies within β = 1.1–1.2 and θ = 45°.

Figure 5

(a) Normalized pull-off stress as a function of χ for β = 1.1 and θ = {25°, 45°, 60°, 80°}. (b) Normalized stress at the tip for Δ/h = 0.0217 for the same β and θ as in (a). A cohesive zone is present at the edge both for θ = 60° and θ = 80°, while it has not formed for θ = 25° and θ = 45° yet.

Figure 6

(a) Simulation results (triangle markers) for β = 1.2, θ = 80° for which a crack initiates at the edge for all χ. Solid line represents Equation 2a with B_e = 0.84 and α = 0.36. Also included are the simulation results (circle markers) for β = 1.2 and θ = 45° for which a crack initiates at the center for all χ. Dashed line represents Equation 2b with B_c = 0.076 and Γ_c = 0.85. (b) Simulation results for β = 1.4, θ = 60° for which a crack initiates at the edge for χ > 7 and at the center for χ < 7. Solid line represents Equation 2a with B_e = 1.2 and α = 0.21. Dashed line represents Equation 2b with B_c = 0.17 and Γ_c = 0.68.

Figure 7

(left) Illustration of three different wedge angles for the mushroom-tipped fibers with β = 1.2 and θ = 45°. (right) Simulation results for 45° wedge (diamond markers), 90° wedge (square markers), and rounded wedge (circular markers).