Opinion dynamics with confirmation bias
- PMID: 25007078
- PMCID: PMC4090078
- DOI: 10.1371/journal.pone.0099557
Opinion dynamics with confirmation bias
Abstract
Background: Confirmation bias is the tendency to acquire or evaluate new information in a way that is consistent with one's preexisting beliefs. It is omnipresent in psychology, economics, and even scientific practices. Prior theoretical research of this phenomenon has mainly focused on its economic implications possibly missing its potential connections with broader notions of cognitive science.
Methodology/principal findings: We formulate a (non-Bayesian) model for revising subjective probabilistic opinion of a confirmationally-biased agent in the light of a persuasive opinion. The revision rule ensures that the agent does not react to persuasion that is either far from his current opinion or coincides with it. We demonstrate that the model accounts for the basic phenomenology of the social judgment theory, and allows to study various phenomena such as cognitive dissonance and boomerang effect. The model also displays the order of presentation effect-when consecutively exposed to two opinions, the preference is given to the last opinion (recency) or the first opinion (primacy) -and relates recency to confirmation bias. Finally, we study the model in the case of repeated persuasion and analyze its convergence properties.
Conclusions: The standard Bayesian approach to probabilistic opinion revision is inadequate for describing the observed phenomenology of persuasion process. The simple non-Bayesian model proposed here does agree with this phenomenology and is capable of reproducing a spectrum of effects observed in psychology: primacy-recency phenomenon, boomerang effect and cognitive dissonance. We point out several limitations of the model that should motivate its future development.
Conflict of interest statement
Figures
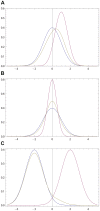
 is described by Gaussian probability density p(x) (blue curve) centered at zero; see (17). The opinion of
is described by Gaussian probability density p(x) (blue curve) centered at zero; see (17). The opinion of  amounts to Gaussian probability density q(x) (purple curve) centered at a positive value. For all three figures continuous density f(x) (
amounts to Gaussian probability density q(x) (purple curve) centered at a positive value. For all three figures continuous density f(x) ( ) were approximated by 100 points
) were approximated by 100 points  ,
,  . The resulting opinion
. The resulting opinion  of
of  is given by (16) with
is given by (16) with  (olive curve). (a) The opinion of
(olive curve). (a) The opinion of  moves towards that of
moves towards that of  ;
;  ,
,  ,
,  ,
,  . (b) The maximally probable opinion of
. (b) The maximally probable opinion of  is reinforced;
is reinforced;  ,
,  ,
,  ,
,  . (c) The change of the opinion of
. (c) The change of the opinion of  is relatively small provided that the Gaussian densities overlap only in the region of non-commitment; cf. (18), (19). Whenever the densities overlap only within the rejection range the difference between p(x) and
is relatively small provided that the Gaussian densities overlap only in the region of non-commitment; cf. (18), (19). Whenever the densities overlap only within the rejection range the difference between p(x) and  is not visible by eyes. For example, if p(x) and q(x) are Gaussian with, respectively,
is not visible by eyes. For example, if p(x) and q(x) are Gaussian with, respectively,  ,
,  ,
,  , the Hellinger distance (see (30) for definition)
, the Hellinger distance (see (30) for definition)  is close to maximally far, while the opinion change is small:
is close to maximally far, while the opinion change is small:  .
.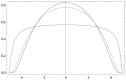
 given by (28) with b = 1. Purple curve: the opinion of
given by (28) with b = 1. Purple curve: the opinion of  described by (28) with
described by (28) with  . Olive curve: the resulting opinion of
. Olive curve: the resulting opinion of  obtained via (16) with
obtained via (16) with  .
.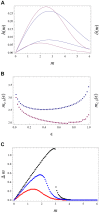
 between the old and new opinion of
between the old and new opinion of  (blue curves); see (30) for the definition. For comparison we also include the total variance distance
(blue curves); see (30) for the definition. For comparison we also include the total variance distance  (purple curves); see (33). These two distances are plotted versus the discrepancy
(purple curves); see (33). These two distances are plotted versus the discrepancy  . The initial opinion of the agent
. The initial opinion of the agent  is Gaussian with
is Gaussian with  and
and  ; see (17). The opinion of
; see (17). The opinion of  is Gaussian with
is Gaussian with  and
and  . Thus m quantifies the initial distance between the opinions of
. Thus m quantifies the initial distance between the opinions of  and
and  . The final opinion
. The final opinion  is given by (13). Different curves correspond to different
is given by (13). Different curves correspond to different  . Blue curves:
. Blue curves:  for
for  (upper curve) and
(upper curve) and  (lower curve). Purple curves:
(lower curve). Purple curves:  for
for  (upper curve) and
(upper curve) and  (lower curve). The maximum of h(m) (
(lower curve). The maximum of h(m) ( ) is reached at
) is reached at  (
( ). (b)
). (b)  (
( ) is the point where h(m) (
) is the point where h(m) ( ) achieves its maximum as a function of m. Blues points:
) achieves its maximum as a function of m. Blues points:  versus
versus  for same parameters as in (a).
for same parameters as in (a).  grows both for
grows both for  and
and  , e.g.
, e.g.  ,
,  ,
,  ,
,  . Purple points:
. Purple points:  versus
versus  for same parameters as in (a). (c) The difference of the anchors (maximally probable values)
for same parameters as in (a). (c) The difference of the anchors (maximally probable values)  versus
versus  for the initial opinions of
for the initial opinions of  and
and  given by (17) under
given by (17) under  ,
,  ,
,  and
and  . The final opinion
. The final opinion  of
of  (and its maximally probable value
(and its maximally probable value  ) if found from (13) under
) if found from (13) under  (black points),
(black points),  (blue points) and
(blue points) and  (red points).
(red points).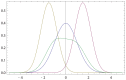
 is described by Gaussian probability density p(x) with
is described by Gaussian probability density p(x) with  and
and  ; see (17). Purple (resp. olive) curve: the initial opinion of
; see (17). Purple (resp. olive) curve: the initial opinion of  (resp.
(resp.  ) are given by (17) with
) are given by (17) with  (resp.
(resp.  ) and
) and  (resp.
(resp.  ). Green curve: the resulting opinion of
). Green curve: the resulting opinion of  after interacting first with
after interacting first with  and then with
and then with  . Both interactions use
. Both interactions use  . The final opinion of
. The final opinion of  is inclined to the most recent opinion (that of
is inclined to the most recent opinion (that of  ) both with respect to its maximally probable value and distance. The final opinion of
) both with respect to its maximally probable value and distance. The final opinion of  has a larger width than the initial one.
has a larger width than the initial one.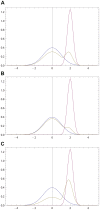
 (resp.
(resp.  ) described by probability density p(x) (resp. q(x)). Olive curve: the final opinion
) described by probability density p(x) (resp. q(x)). Olive curve: the final opinion  of
of  as given by (16) with
as given by (16) with  . Here p(x) and q(x) are defined by (17) with
. Here p(x) and q(x) are defined by (17) with  ,
,  ,
,  ,
,  . The final opinion develops two peaks of comparable height (cognitive dissonance). (b) Avoiding the cognitive dissonance due to a larger
. The final opinion develops two peaks of comparable height (cognitive dissonance). (b) Avoiding the cognitive dissonance due to a larger  : the second peak is much smaller (other parameters are those of (a)). (c) Avoiding the cognitive dissonance due to a smaller
: the second peak is much smaller (other parameters are those of (a)). (c) Avoiding the cognitive dissonance due to a smaller  : the first peak is much smaller (other parameters are those of (a)).
: the first peak is much smaller (other parameters are those of (a)).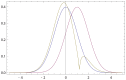
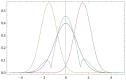
 (resp.
(resp.  ) described by probability density p(x) (resp. q(x)). Olive curve: the final opinion
) described by probability density p(x) (resp. q(x)). Olive curve: the final opinion  of
of  given by (16) with
given by (16) with  . Here p(x) and q(x) are given by (17) with
. Here p(x) and q(x) are given by (17) with  and
and  . The anchor (maximally probable opinion) of
. The anchor (maximally probable opinion) of  not only moves away from the anchor of
not only moves away from the anchor of  ; but it is also enhanced: the (biggest) peak of
; but it is also enhanced: the (biggest) peak of  is larger than that of p(x). The second (smaller) peak of
is larger than that of p(x). The second (smaller) peak of  arises because the initial probability of
arises because the initial probability of  located to the right from the anchor
located to the right from the anchor  of
of  , moves away from
, moves away from  ;
;  gets a local minimum close to
gets a local minimum close to  .
.
 (boomerang regime). Now the final opinion of
(boomerang regime). Now the final opinion of  is inclined to the first opinion (that of
is inclined to the first opinion (that of  ) with respect to the distance. The initial maximally probable opinion of
) with respect to the distance. The initial maximally probable opinion of  is still maximally probable. Moreover, its probability has increased and the width around it has decreased. The final opinion has 3 peaks.
is still maximally probable. Moreover, its probability has increased and the width around it has decreased. The final opinion has 3 peaks.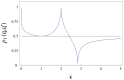
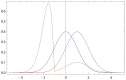
 given by (50, 51) versus
given by (50, 51) versus  .
.
 (resp.
(resp.  ) described by probability density p(x) (resp. q(x)) as given by (17) with
) described by probability density p(x) (resp. q(x)) as given by (17) with  ,
,  ,
,  . Olive curve: the opinion of
. Olive curve: the opinion of  after 50 iterations (52) with
after 50 iterations (52) with  .
.References
-
- Abelson RP (1986) Beliefs are like possessions. Journal for the Theory of Social Behaviour 16: 223–250.
-
- Akerlof G, Dickens WT (1982) The economic consequences of cognitive dissonance. Amer. Econ. Rev. 72: 307–319.
-
- Alchourrón CE, Gärdenfors G, Makinsin D (1985) On the logic of theory change. J. Symb. Logic 50: 510–530.
-
- Allahverdyan AE, Galstyan A (2011) Le Chatelier principle in replicator dynamics. Physical Review E 84: 041117. - PubMed
-
- Allakhverdov VM, Gershkovich VA (2010) Does consciousness exist? in what sense? Integrative Psychological and Behavioral Science 44: 340–347. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

