Interplay between short- and long-term plasticity in cell-assembly formation
- PMID: 25007209
- PMCID: PMC4090127
- DOI: 10.1371/journal.pone.0101535
Interplay between short- and long-term plasticity in cell-assembly formation
Abstract
Various hippocampal and neocortical synapses of mammalian brain show both short-term plasticity and long-term plasticity, which are considered to underlie learning and memory by the brain. According to Hebb's postulate, synaptic plasticity encodes memory traces of past experiences into cell assemblies in cortical circuits. However, it remains unclear how the various forms of long-term and short-term synaptic plasticity cooperatively create and reorganize such cell assemblies. Here, we investigate the mechanism in which the three forms of synaptic plasticity known in cortical circuits, i.e., spike-timing-dependent plasticity (STDP), short-term depression (STD) and homeostatic plasticity, cooperatively generate, retain and reorganize cell assemblies in a recurrent neuronal network model. We show that multiple cell assemblies generated by external stimuli can survive noisy spontaneous network activity for an adequate range of the strength of STD. Furthermore, our model predicts that a symmetric temporal window of STDP, such as observed in dopaminergic modulations on hippocampal neurons, is crucial for the retention and integration of multiple cell assemblies. These results may have implications for the understanding of cortical memory processes.
Conflict of interest statement
Figures

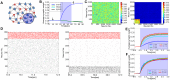









 : the boundaries were decided such that each group contains 5 to 15 assemblies) and calculated the fraction of the assemblies that survived in the reorganization. See Methods for other details of the simulations. (F) The rate of merging of a cell assembly as a function of the initial synaptic weight. As in E, we separated 992 inter-assembly connections into five groups (
: the boundaries were decided such that each group contains 5 to 15 assemblies) and calculated the fraction of the assemblies that survived in the reorganization. See Methods for other details of the simulations. (F) The rate of merging of a cell assembly as a function of the initial synaptic weight. As in E, we separated 992 inter-assembly connections into five groups (



 ) so that each group contains more than 100 assemblies.
) so that each group contains more than 100 assemblies.Similar articles
-
Long-term population spike-timing-dependent plasticity promotes synaptic tagging but not cross-tagging in rat hippocampal area CA1.Proc Natl Acad Sci U S A. 2019 Mar 19;116(12):5737-5746. doi: 10.1073/pnas.1817643116. Epub 2019 Feb 28. Proc Natl Acad Sci U S A. 2019. PMID: 30819889 Free PMC article.
-
[Acquiring new information in a neuronal network: from Hebb's concept to homeostatic plasticity].J Soc Biol. 2008;202(2):143-60. doi: 10.1051/jbio:2008018. Epub 2008 Jun 13. J Soc Biol. 2008. PMID: 18547512 Review. French.
-
Intrinsic stability of temporally shifted spike-timing dependent plasticity.PLoS Comput Biol. 2010 Nov 4;6(11):e1000961. doi: 10.1371/journal.pcbi.1000961. PLoS Comput Biol. 2010. PMID: 21079671 Free PMC article.
-
Modulation of synaptic plasticity by the coactivation of spatially distinct synaptic inputs in rat hippocampal CA1 apical dendrites.Brain Res. 2013 Aug 14;1526:1-14. doi: 10.1016/j.brainres.2013.05.023. Epub 2013 May 24. Brain Res. 2013. PMID: 23711890
-
Temporal asymmetry in spike timing-dependent synaptic plasticity.Physiol Behav. 2002 Dec;77(4-5):551-5. doi: 10.1016/s0031-9384(02)00933-2. Physiol Behav. 2002. PMID: 12526998 Review.
Cited by
-
Reduced presynaptic vesicle stores mediate cellular and network plasticity defects in an early-stage mouse model of Alzheimer's disease.Mol Neurodegener. 2019 Jan 22;14(1):7. doi: 10.1186/s13024-019-0307-7. Mol Neurodegener. 2019. PMID: 30670054 Free PMC article.
-
Biphasic Cholinergic Modulation of Reverberatory Activity in Neuronal Networks.Neurosci Bull. 2023 May;39(5):731-744. doi: 10.1007/s12264-022-01012-7. Epub 2023 Jan 21. Neurosci Bull. 2023. PMID: 36670292 Free PMC article.
-
Endogenous neurosteroids pregnanolone and pregnanolone sulfate potentiate presynaptic glutamate release through distinct mechanisms.Br J Pharmacol. 2021 Oct;178(19):3888-3904. doi: 10.1111/bph.15529. Epub 2021 Jun 22. Br J Pharmacol. 2021. PMID: 33988248 Free PMC article.
-
Mixed signal learning by spike correlation propagation in feedback inhibitory circuits.PLoS Comput Biol. 2015 Apr 24;11(4):e1004227. doi: 10.1371/journal.pcbi.1004227. eCollection 2015 Apr. PLoS Comput Biol. 2015. PMID: 25910189 Free PMC article.
-
Drifting assemblies for persistent memory: Neuron transitions and unsupervised compensation.Proc Natl Acad Sci U S A. 2021 Nov 16;118(46):e2023832118. doi: 10.1073/pnas.2023832118. Proc Natl Acad Sci U S A. 2021. PMID: 34772802 Free PMC article.
References
-
- Hebb DO (1949) The organization of behavior: a neuropsychological theory. New York: Wiley.
-
- O’Neill J, Pleydell-Bouverie B, Dupret D, Csicsvari J (2010) Play it again: reactivation of waking experience and memory. Trends Neurosci 33: 220–229. - PubMed
-
- Diekelmann S, Born J (2010) The memory function of sleep. Nat Rev Neurosci 11: 114–126. - PubMed
-
- Lewis PA, Durrant SJ (2011) Overlapping memory replay during sleep builds cognitive schemata. Trends Neurosci 15: 343–351. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

