Random and targeted interventions for epidemic control in metapopulation models
- PMID: 25026972
- PMCID: PMC4099978
- DOI: 10.1038/srep05522
Random and targeted interventions for epidemic control in metapopulation models
Abstract
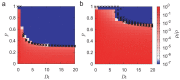
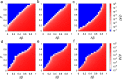
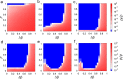
In general, different countries and communities respond to epidemics in accordance with their own control plans and protocols. However, owing to global human migration and mobility, strategic planning for epidemic control measures through the collaboration of relevant public health administrations is gaining importance for mitigating and containing large-scale epidemics. Here, we present a framework to evaluate the effectiveness of random (non-strategic) and targeted (strategic) epidemic interventions for spatially separated patches in metapopulation models. For a random intervention, we analytically derive the critical fraction of patches that receive epidemic interventions, above which epidemics are successfully contained. The analysis shows that the heterogeneity of patch connectivity makes it difficult to contain epidemics under the random intervention. We demonstrate that, particularly in such heterogeneously connected networks, targeted interventions are considerably effective compared to the random intervention. Our framework is useful for identifying the target areas where epidemic control measures should be focused.
Figures

 and that in the low-risk patches by
and that in the low-risk patches by  . The parameter p represents the ratio of the low-risk patches to the whole patches, corresponding to the total size of public health interventions.
. The parameter p represents the ratio of the low-risk patches to the whole patches, corresponding to the total size of public health interventions.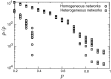

Similar articles
-
Intervention threshold for epidemic control in susceptible-infected-recovered metapopulation models.Phys Rev E. 2019 Aug;100(2-1):022302. doi: 10.1103/PhysRevE.100.022302. Phys Rev E. 2019. PMID: 31574659 Free PMC article.
-
Epidemic modeling in metapopulation systems with heterogeneous coupling pattern: theory and simulations.J Theor Biol. 2008 Apr 7;251(3):450-67. doi: 10.1016/j.jtbi.2007.11.028. Epub 2007 Nov 29. J Theor Biol. 2008. PMID: 18222487
-
Network structure-based interventions on spatial spread of epidemics in metapopulation networks.Phys Rev E. 2020 Dec;102(6-1):062306. doi: 10.1103/PhysRevE.102.062306. Phys Rev E. 2020. PMID: 33466001
-
epiDMS: Data Management and Analytics for Decision-Making From Epidemic Spread Simulation Ensembles.J Infect Dis. 2016 Dec 1;214(suppl_4):S427-S432. doi: 10.1093/infdis/jiw305. J Infect Dis. 2016. PMID: 28830107 Free PMC article. Review.
-
Trends of major disease outbreaks in the African region, 2003-2007.East Afr J Public Health. 2010 Mar;7(1):20-9. doi: 10.4314/eajph.v7i1.64672. East Afr J Public Health. 2010. PMID: 21413568 Review.
Cited by
-
The Scaling of Human Contacts and Epidemic Processes in Metapopulation Networks.Sci Rep. 2015 Oct 19;5:15111. doi: 10.1038/srep15111. Sci Rep. 2015. PMID: 26478209 Free PMC article.
-
Parameter Scaling for Epidemic Size in a Spatial Epidemic Model with Mobile Individuals.PLoS One. 2016 Dec 14;11(12):e0168127. doi: 10.1371/journal.pone.0168127. eCollection 2016. PLoS One. 2016. PMID: 27973605 Free PMC article.
-
A straightforward edge centrality concept derived from generalizing degree and strength.Sci Rep. 2022 Mar 15;12(1):4407. doi: 10.1038/s41598-022-08254-5. Sci Rep. 2022. PMID: 35292696 Free PMC article.
-
Voluntary Vaccination through Self-organizing Behaviors on Locally-mixed Social Networks.Sci Rep. 2017 Jun 1;7(1):2665. doi: 10.1038/s41598-017-02967-8. Sci Rep. 2017. PMID: 28572623 Free PMC article.
-
Intervention threshold for epidemic control in susceptible-infected-recovered metapopulation models.Phys Rev E. 2019 Aug;100(2-1):022302. doi: 10.1103/PhysRevE.100.022302. Phys Rev E. 2019. PMID: 31574659 Free PMC article.
References
-
- United States Centers for Disease Control and Prevention. A CDC Framework for Preventing Infectious Diseases. Available at http://www.cdc.gov/oid/framework.html (last accessed January 10 2013).
-
- Hitchcock P., Chamberlain A., Van Wagoner M., Inglesby T. V. & O'Toole T. Challenges to global surveillance and response to infectious disease outbreaks of international importance. Biosecur. Bioterror. 5, 206–227 (2007). - PubMed
-
- Global Outbreak Alert & Response Network. Available at http://www.who.int/csr/outbreaknetwork/en/ (last accessed February 2 2014).
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

