Conformational mechanism for the stability of microtubule-kinetochore attachments

Abstract

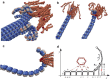
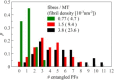
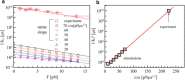
Regulating the stability of microtubule (MT)-kinetochore attachments is fundamental to avoiding mitotic errors and ensuring proper chromosome segregation during cell division. Although biochemical factors involved in this process have been identified, their mechanics still need to be better understood. Here we introduce and simulate a mechanical model of MT-kinetochore interactions in which the stability of the attachment is ruled by the geometrical conformations of curling MT-protofilaments entangled in kinetochore fibrils. The model allows us to reproduce, with good accuracy, in vitro experimental measurements of the detachment times of yeast kinetochores from MTs under external pulling forces. Numerical simulations suggest that geometrical features of MT-protofilaments may play an important role in the switch between stable and unstable attachments.

Figure 1

Three-dimensional tubulin block model of the MT. (a) A tubulin block consists of eight nodes connected to neighboring nodes via stiff linear springs. Diagonal struts are added to avoid shearing and twisting. Each node is also endowed with a hard-core repelling potential. The top and bottom faces of the blocks are of trapezoidal shape to induce lateral curvature in the MT. (b) A PF is obtained by arranging tubulin blocks along a line and connecting them with springs. PFs can be straight or bent, depending on the ratio of top/bottom lengths of the block. (c) A sheet of tubulin blocks will form a tubular structure when the opposing sides of the block are trapezoidal. In this case we have d₂ > d₁ and d₃ = d₄, corresponding to a GTP-bound MT. The sheet will fold with a helicity depending on the number of transversal units and the ratio d₂/d₁. (d) Clamping one end of the MT while hydrolyzing the blocks by letting d₃ > d₄ and allowing transversal bonds to break leads to the ram’s-horn shape typical of depolymerizing MTs. To see this figure in color, go online.

Figure 2

Summary of the model for the kinetochore-MT interface. (a) The fully hydrolyzed PFs of the MT curl, forming ram’s horns, locking into loops formed by the kinetochore fibrils. (b) Genesis of a loop by fibrils attaching to the not-yet-hydrolyzed tubulin block, and locking into each other. When the tubulin blocks are hydrolyzed, the curling links the PF tip into the fibrils loop. (c and d) Side-view of a PF tip with kinetochore-fibril loops around it and its two-dimensional reduction. To see this figure in color, go online.

Figure 3

Histogram of the number of entangled PFs interacting with a set of kinetochore fibrils for three different densities. The total number of simulations is 30 in all cases. For details, see text. To see this figure in color, go online.

Figure 4

Detachment mechanisms of the kinetochore-PF interface. (a) Force-displacement curve of a straight PF-kinetochore fibrils interface. The fibrils are attached to the first tubulin block of the PF because the fibril tips interact with the PF via a Lennard-Jones potential with strength ϵ(F-P). Displacing the fibril ends leads at first to no increase of the force as long as the fibril unwraps. Upon completion of this straightening process, the force increases rapidly as the fibrils and the PF stretch while overcoming Lennard-Jones attraction. (b) Force-displacement curve of a GDP-tubulin PF in the curved conformation. Again, the kinetochore fibrils are pulled with constant velocity and the in-line component of the interaction force is plotted for flexural rigidity B = 5 × 10⁴ pN nm² and B = 1.5 × 10⁴ pN nm². The interaction energy between the fibrils is modeled by a Lennard-Jones potential with ϵ(F-F) $=500$ pN nm or ϵ(F-F) $=100$ pN nm. In the first case, the peak corresponds to the bending of the PF and in the second case, to the breakdown of the fibril loop. The oscillation (black curve) is due to the discrete nature of the PF and arises from the sliding of the kinetochore fibrils from one block to the next. This oscillation is drowned out by noise when the flexural rigidity is reduced (as shown in the red curve). To see this figure in color, go online.

Figure 5

Simulation of the catch-bond behavior for depolymerizing PFs. (a) The detachment rate as a function of the pulling force for different values of the diffusion parameter ω for the two-dimensional model of a depolymerizing PF together with the experimental data from Akiyoshi et al. (29). (b) Extrapolation of the diffusion parameter ω in the experiments from the numerical data. (c) Attachment lifetimes (inverse detachment rates) of depolymerizing PFs to kinetochores at high forces. The numerical data suggests that the lifetime peaks due to deformations and then decreases sharply with applied load. The low-force parts and the peaks can be fitted well with the Weibull distribution, which yields also a reasonable fit for the experimental data, as shown in panel d. To see this figure in color, go online.

Figure 6

Detachment from a growing PF. (a) Attachment lifetimes obtained for the two-dimensional model for polymerizing PFs as a function of the binding strength-fluctuation ratio ϵ/ω together with the experimental data from Akiyoshi et al. (29). For a sufficiently high binding strength/fluctuation ratio, the parameter F₃, appearing as the slope here, stays constant and is the same for the numerical and experimental data. (b) Extrapolation of the experimentally observed binding strength. To see this figure in color, go online.