Learning Instance-Specific Predictive Models
- PMID: 25045325
- PMCID: PMC4102007
Learning Instance-Specific Predictive Models
Abstract
This paper introduces a Bayesian algorithm for constructing predictive models from data that are optimized to predict a target variable well for a particular instance. This algorithm learns Markov blanket models, carries out Bayesian model averaging over a set of models to predict a target variable of the instance at hand, and employs an instance-specific heuristic to locate a set of suitable models to average over. We call this method the instance-specific Markov blanket (ISMB) algorithm. The ISMB algorithm was evaluated on 21 UCI data sets using five different performance measures and its performance was compared to that of several commonly used predictive algorithms, including nave Bayes, C4.5 decision tree, logistic regression, neural networks, k-Nearest Neighbor, Lazy Bayesian Rules, and AdaBoost. Over all the data sets, the ISMB algorithm performed better on average on all performance measures against all the comparison algorithms.
Keywords: Bayesian model averaging; Bayesian network; Markov blanket; instance-specific.
Figures
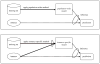

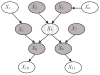

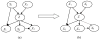



References
-
- Aha DW. Feature weighting for lazy learning algorithms. In: Huan L, Hiroshi M, editors. Feature Extraction, Construction and Selection: A Data Mining Perspective. Kluwer Academic Publisher; Norwell, MA: 1998. pp. 13–32.
-
- Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD. Local causal and markov blanket induction for causal discovery and feature selection for classification part i: Algorithms and empirical evaluation. Journal of Machine Learning Research. 2010a Jan;11:171–234.
-
- Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD. Local causal and markov blanket induction for causal discovery and feature selection for classification part ii: Analysis and extensions. Journal of Machine Learning Research. 2010b Jan;11:235–284.
-
- Atkeson CG, Moore AW, Schaal S. Locally weighted learning. Artificial Intelligence Review. 1997;11(1–5):11–73.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
