"Magnitude-based inference": a statistical review
- PMID: 25051387
- PMCID: PMC5642352
- DOI: 10.1249/MSS.0000000000000451
"Magnitude-based inference": a statistical review
Abstract
Purpose: We consider "magnitude-based inference" and its interpretation by examining in detail its use in the problem of comparing two means.
Methods: We extract from the spreadsheets, which are provided to users of the analysis (http://www.sportsci.org/), a precise description of how "magnitude-based inference" is implemented. We compare the implemented version of the method with general descriptions of it and interpret the method in familiar statistical terms.
Results and conclusions: We show that "magnitude-based inference" is not a progressive improvement on modern statistics. The additional probabilities introduced are not directly related to the confidence interval but, rather, are interpretable either as P values for two different nonstandard tests (for different null hypotheses) or as approximate Bayesian calculations, which also lead to a type of test. We also discuss sample size calculations associated with "magnitude-based inference" and show that the substantial reduction in sample sizes claimed for the method (30% of the sample size obtained from standard frequentist calculations) is not justifiable so the sample size calculations should not be used. Rather than using "magnitude-based inference," a better solution is to be realistic about the limitations of the data and use either confidence intervals or a fully Bayesian analysis.
Figures
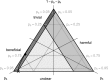

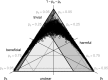
Comment in
-
Magnitude-based inference: progressive approach or flawed statistic?Med Sci Sports Exerc. 2015 Apr;47(4):873. doi: 10.1249/MSS.0000000000000467. Med Sci Sports Exerc. 2015. PMID: 25783665 No abstract available.
-
The case for magnitude-based inference.Med Sci Sports Exerc. 2015 Apr;47(4):885. doi: 10.1249/MSS.0000000000000551. Med Sci Sports Exerc. 2015. PMID: 25783666 No abstract available.
-
Response.Med Sci Sports Exerc. 2015 Apr;47(4):886. doi: 10.1249/MSS.0000000000000552. Med Sci Sports Exerc. 2015. PMID: 25783667 No abstract available.
References
-
- Altman DG, Machin D, Bryant TN, Gardner MJ. Statistics with Confidence: Confidence Intervals and Statistical Guidelines. 2nd ed New York (NY): Wiley; 2000. pp. 1– 254.
-
- Baguley T. Standardized or simple effect size: what should be reported? Br J Psychol. 2009; 100: 603– 17. - PubMed
-
- Barker RJ, Schofield MR. Inferences about magnitudes of effects. Int J Sports Physiol Perform 2008; 3: 547– 57. - PubMed
-
- Batterham AM, Hopkins WG. Making meaningful inferences about magnitudes. Sportscience. 2005; 9: 6– 13. - PubMed
-
- Batterham AM, Hopkins WG. Making meaningful inferences about magnitudes. Int J Sports Physiol Perform. 2006; 1: 50– 7. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
Molecular Biology Databases

