Identifying keystone species in the human gut microbiome from metagenomic timeseries using sparse linear regression

Abstract

Human associated microbial communities exert tremendous influence over human health and disease. With modern metagenomic sequencing methods it is now possible to follow the relative abundance of microbes in a community over time. These microbial communities exhibit rich ecological dynamics and an important goal of microbial ecology is to infer the ecological interactions between species directly from sequence data. Any algorithm for inferring ecological interactions must overcome three major obstacles: 1) a correlation between the abundances of two species does not imply that those species are interacting, 2) the sum constraint on the relative abundances obtained from metagenomic studies makes it difficult to infer the parameters in timeseries models, and 3) errors due to experimental uncertainty, or mis-assignment of sequencing reads into operational taxonomic units, bias inferences of species interactions due to a statistical problem called "errors-in-variables". Here we introduce an approach, Learning Interactions from MIcrobial Time Series (LIMITS), that overcomes these obstacles. LIMITS uses sparse linear regression with boostrap aggregation to infer a discrete-time Lotka-Volterra model for microbial dynamics. We tested LIMITS on synthetic data and showed that it could reliably infer the topology of the inter-species ecological interactions. We then used LIMITS to characterize the species interactions in the gut microbiomes of two individuals and found that the interaction networks varied significantly between individuals. Furthermore, we found that the interaction networks of the two individuals are dominated by distinct "keystone species", Bacteroides fragilis and Bacteroided stercosis, that have a disproportionate influence on the structure of the gut microbiome even though they are only found in moderate abundance. Based on our results, we hypothesize that the abundances of certain keystone species may be responsible for individuality in the human gut microbiome.

Figure 1. There is no simple relation between interaction coefficients and correlations in abundance.

a) A symmetric interaction matrix and the corresponding correlation matrix. b) There is no relation between the interaction parameters and the correlations in abundance for the symmetric interaction matrix. c) An asymmetric interaction matrix and the corresponding correlation matrix. d) There is no relation between the interaction parameters and the correlations in abundance for the asymmetric interaction matrix. Points from above the diagonal in the interaction matrix are gray circles, whereas points from below the diagonal are black squares. 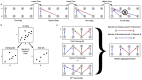In a and c, matrix elements have been scaled so that the smallest negative element is , the largest positive element is , and all elements retain their sign. In b and d, interaction coefficents were scaled so that the largest element by absolute value has .

Figure 2. Schematic illustrating forward stepwise regression and median bootstrap aggregating.

a) In forward stepwise regression, interactions are added to the model one at a time as long as including the additional covariate lowers the prediction error by a pre-defined threshold. b) The prediction error used for variable selection is evaluated by randomly partitioning the data into a training set used for the regression and a test used to evaluate the prediction error. c) Multiple models are built by repeatedly applying forward stepwise regression to random partitions of the data, each containing half the data points. The models are aggregated, or “bagged”, by taking the median, which improves the stability of the fit while preserving the sparsity of the inferred interactions.

Figure 3. Example fits of interaction parameters using sparse linear regression.

a) A symmetric interaction matrix (left), the corresponding matrix inferred from absolute abundance data (middle), and the corresponding matrix inferred from relative abundance data (right). b) There is good aggreement between the true and inferred interactions, from both absolute (black) and relative (gray) abundances, for the symmetric interaction matrix. c) An asymmetric interaction matrix (left), the corresponding matrix inferred from absolute abundance data (middle), and the corresponding matrix inferred from relative abundance data (right). d) There is good aggreement between the true and inferred interactions, from both absolute (black) and relative (gray) abundances, for the asymmetric interaction matrix. The prediction error threshold was set to 5% in for all fits.

Figure 4. Performance of sparse linear regression as a functon of sample size and the prediction error threshold.

a) Performance on absolute (red) and relative (black) abundances as a function of sample size for symmetric interaction matrices. b) Performance on absolute (red) and relative (black) abundances as a function of sample size for asymmetric interaction matrices. c) Performance on absolute (red) and relative (black) abundances as a function of the out-of-bag error threshold for symmetric interaction matrices. d) Performance on absolute (red) and relative (black) abundances as a function of the out-of-bag error threshold for symmetric interaction matrices. Error bars correspond to one standard deviation, and lines connect the means.

Figure 5. Sensitivity and specificity of predicted interactions as a function of measurement error for bagged and unbagged models.

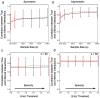
Specificity refers to the fraction of species pairs correctly identified as non-interacting, while sensitivity refers to the fraction of species pairs correctly identified as interaction. Both measures range from (poor performance) to (good performance). a) Specifity of sparse linear regression with Bagging as a function of measurement error for different prediction error thresholds. b) Specificity of sparse linear regression trained on the entire data set without Bagging as a function of measurement error for different prediction thresholds. c) Sensitivity of sparse linear regression with Bagging as a function of measurement error for different prediction error thresholds. d) Sensitivity of sparse linear regression trained on the entire data set without Bagging as a function of measurement error for different prediction error thresholds. Notice that without bagging, model performance is extremely sensitive to choice of the threshold for the required improvement in prediction for adding new interactions.

Figure 6. Interaction topologies of abundant species in the guts of two individuals.

The size of a node denotes the median relative species abundance, beneficial interactions are shown as solid red arrows, and competetive interactions are shown as dashed blue arrows. In individual a) species 4 Bacteroides fragilis acts as a keystone species with 6 outgoing interactions, compared to a median number of outgoing interactions of . In individual b) species 5 Bacteroides stercosis acts as a keystone species with 4 outgoing interactions, compared a median number of outgoing interactions of . The 14 species included in the model were obtained by taking the union of the top 10 most abundant species from individuals a and b. The required improvement in prediction was set to 3%, graphs obtained using other prediction thresholds are shown in the Supporting Information.