From spontaneous motor activity to coordinated behaviour: a developmental model
- PMID: 25057775
- PMCID: PMC4109855
- DOI: 10.1371/journal.pcbi.1003653
From spontaneous motor activity to coordinated behaviour: a developmental model
Abstract
In mammals, the developmental path that links the primary behaviours observed during foetal stages to the full fledged behaviours observed in adults is still beyond our understanding. Often theories of motor control try to deal with the process of incremental learning in an abstract and modular way without establishing any correspondence with the mammalian developmental stages. In this paper, we propose a computational model that links three distinct behaviours which appear at three different stages of development. In order of appearance, these behaviours are: spontaneous motor activity (SMA), reflexes, and coordinated behaviours, such as locomotion. The goal of our model is to address in silico four hypotheses that are currently hard to verify in vivo: First, the hypothesis that spinal reflex circuits can be self-organized from the sensor and motor activity induced by SMA. Second, the hypothesis that supraspinal systems can modulate reflex circuits to achieve coordinated behaviour. Third, the hypothesis that, since SMA is observed in an organism throughout its entire lifetime, it provides a mechanism suitable to maintain the reflex circuits aligned with the musculoskeletal system, and thus adapt to changes in body morphology. And fourth, the hypothesis that by changing the modulation of the reflex circuits over time, one can switch between different coordinated behaviours. Our model is tested in a simulated musculoskeletal leg actuated by six muscles arranged in a number of different ways. Hopping is used as a case study of coordinated behaviour. Our results show that reflex circuits can be self-organized from SMA, and that, once these circuits are in place, they can be modulated to achieve coordinated behaviour. In addition, our results show that our model can naturally adapt to different morphological changes and perform behavioural transitions.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
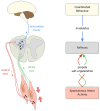
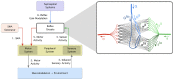
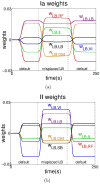
 ) and secondary (
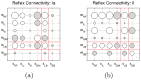
) and secondary ( ) spindle afferent fibers. 4) The correlation between the sensor and motor signals is used to self-organize the reflex networks,
) spindle afferent fibers. 4) The correlation between the sensor and motor signals is used to self-organize the reflex networks,  and
and  which mediate the connectivity of afferents
which mediate the connectivity of afferents  and
and  respectively. 5) The reflex circuits are modulated from supraspinal systems using gains
respectively. 5) The reflex circuits are modulated from supraspinal systems using gains  and
and  which independently scale the reflex networks
which independently scale the reflex networks  and
and  respectively.
respectively.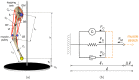
 ), the rectus femoris (
), the rectus femoris ( ), the vastus intermedius (
), the vastus intermedius ( ), the gluteus maximus (
), the gluteus maximus ( ), the long biceps (
), the long biceps ( ), and the short biceps (
), and the short biceps ( );
);  and
and  represent the height of the end-effector and the ground respectively, and
represent the height of the end-effector and the ground respectively, and  represents the height of the hip.
represents the height of the hip. 
 and
and  show the centers of mass of the pelvis, femur and tibia, respectively.
show the centers of mass of the pelvis, femur and tibia, respectively.  and
and  are the lengths of the femur and the tibia, respectively; the centers of mass of these bodies are located in the geometrical center of the body. b) The 3-element muscle model used; it consists of a spring (
are the lengths of the femur and the tibia, respectively; the centers of mass of these bodies are located in the geometrical center of the body. b) The 3-element muscle model used; it consists of a spring ( ) and a damper (
) and a damper ( ) in parallel to the contractile element (
) in parallel to the contractile element ( ).
).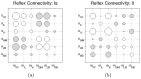
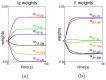


 for type-Ia afferents and
for type-Ia afferents and  for type-II afferents.
for type-II afferents.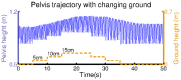

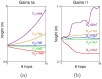
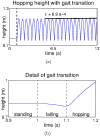
 and c) misplaced
and c) misplaced  S refers to the stance phase (when the end effector is in touch with the ground) and F refers to the flight phase (when the end effector is in the air). The hip trajectory recorded for the system with d) four muscles, e) modified
S refers to the stance phase (when the end effector is in touch with the ground) and F refers to the flight phase (when the end effector is in the air). The hip trajectory recorded for the system with d) four muscles, e) modified  and f) misplaced
and f) misplaced 


 and b) misplaced
and b) misplaced  S refers to the stance phase (when the end effector is in touch with the ground) and F refers to the flight phase (when the end effector is in the air). The hip trajectory recorded for the system with c) misplaced
S refers to the stance phase (when the end effector is in touch with the ground) and F refers to the flight phase (when the end effector is in the air). The hip trajectory recorded for the system with c) misplaced  and d) misplaced
and d) misplaced 
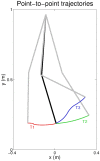
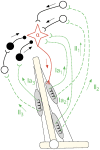
Similar articles
-
Interlimb neural interactions in corticospinal and spinal reflex circuits during preparation and execution of isometric elbow flexion.J Neurophysiol. 2020 Sep 1;124(3):652-667. doi: 10.1152/jn.00705.2019. Epub 2020 Jul 22. J Neurophysiol. 2020. PMID: 32697605
-
Sensory modulation of gait characteristics in human locomotion: A neuromusculoskeletal modeling study.PLoS Comput Biol. 2021 May 19;17(5):e1008594. doi: 10.1371/journal.pcbi.1008594. eCollection 2021 May. PLoS Comput Biol. 2021. PMID: 34010288 Free PMC article.
-
Self-organising bio-inspired reflex circuits for robust motor coordination in artificial musculoskeletal systems.Bioinspir Biomim. 2025 Jun 6;20(4). doi: 10.1088/1748-3190/adde08. Bioinspir Biomim. 2025. PMID: 40436031
-
Contributions to the understanding of gait control.Dan Med J. 2014 Apr;61(4):B4823. Dan Med J. 2014. PMID: 24814597 Review.
-
Tapping into spinal circuits to restore motor function.Brain Res Brain Res Rev. 1999 Jul;30(1):27-51. doi: 10.1016/s0165-0173(99)00008-9. Brain Res Brain Res Rev. 1999. PMID: 10407124 Review.
Cited by
-
Versatile graceful degradation framework for bio-inspired proprioception with redundant soft sensors.Front Robot AI. 2025 Jan 6;11:1504651. doi: 10.3389/frobt.2024.1504651. eCollection 2024. Front Robot AI. 2025. PMID: 39835247 Free PMC article.
-
Roadbumps at the Crossroads of Integrating Behavioral and In Vitro Approaches for Neurotoxicity Assessment.Front Toxicol. 2022 Feb 25;4:812863. doi: 10.3389/ftox.2022.812863. eCollection 2022. Front Toxicol. 2022. PMID: 35295216 Free PMC article. Review.
-
Bayesian action&perception: representing the world in the brain.Front Neurosci. 2014 Oct 30;8:341. doi: 10.3389/fnins.2014.00341. eCollection 2014. Front Neurosci. 2014. PMID: 25400542 Free PMC article. Review.
-
Development of twitching in sleeping infant mice depends on sensory experience.Curr Biol. 2015 Mar 2;25(5):656-62. doi: 10.1016/j.cub.2015.01.022. Epub 2015 Feb 19. Curr Biol. 2015. PMID: 25702578 Free PMC article.
-
Sensory feedback synchronizes motor and sensory neuronal networks in the neonatal rat spinal cord.Nat Commun. 2016 Oct 7;7:13060. doi: 10.1038/ncomms13060. Nat Commun. 2016. PMID: 27713428 Free PMC article.
References
-
- Prechtl HF (1990) Qualitative changes of spontaneous movements in fetus and preterm infant are a marker of neurological dysfunction. Early Hum Dev 23: 151–158. - PubMed
-
- Robinson SR, Brumley M (2005) Prenatal behavior. In: Whishaw IQ, Kolb B, editors, The Behaviour of the Laboratory Rat: A Handbook with Tests, Oxford: Oxford University Press, chapter 24. pp. 257–265.
-
- Brown TG (1911) The intrinsic factors in the act of progression in the mammal. Proc R Soc Lond B 84: 308–319.
-
- Sherrington CS (2010) The Integrative Action of the Nervous System. Nabu Press.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

