Social cycling and conditional responses in the Rock-Paper-Scissors game
- PMID: 25060115
- PMCID: PMC5376050
- DOI: 10.1038/srep05830
Social cycling and conditional responses in the Rock-Paper-Scissors game
Abstract
How humans make decisions in non-cooperative strategic interactions is a big question. For the fundamental Rock-Paper-Scissors (RPS) model game system, classic Nash equilibrium (NE) theory predicts that players randomize completely their action choices to avoid being exploited, while evolutionary game theory of bounded rationality in general predicts persistent cyclic motions, especially in finite populations. However as empirical studies have been relatively sparse, it is still a controversial issue as to which theoretical framework is more appropriate to describe decision-making of human subjects. Here we observe population-level persistent cyclic motions in a laboratory experiment of the discrete-time iterated RPS game under the traditional random pairwise-matching protocol. This collective behavior contradicts with the NE theory but is quantitatively explained, without any adjustable parameter, by a microscopic model of win-lose-tie conditional response. Theoretical calculations suggest that if all players adopt the same optimized conditional response strategy, their accumulated payoff will be much higher than the reference value of the NE mixed strategy. Our work demonstrates the feasibility of understanding human competition behaviors from the angle of non-equilibrium statistical physics.
Conflict of interest statement
The authors declare no competing financial interests.
Figures
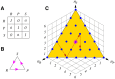
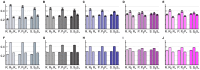
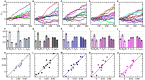
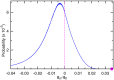
References
-
- Sinervo B. & Lively C. The rock-paper-scissors game and the evolution of alternative male strategies. Nature 380, 240–243 (1996).
-
- Kerr B., Riley M. A., Feldman M. W. & Bohannan B. J. M. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature 418, 171–174 (2002). - PubMed
-
- Semmann D., Krambeck H.-J. & Milinski M. Volunteering leads to rock-paper-scissors dynamics in a public goods game. Nature 425, 390–393 (2003). - PubMed
-
- Lee D., McGreevy B. P. & Barraclough D. J. Learning and decision making in monkeys during a rock-paper-scissors game. Cogn. Brain Res. 25, 416–430 (2005). - PubMed
-
- Reichenbach T., Mobilia M. & Frey E. Mobility promotes and jeopardizes biodiversity in rock-paper-scissors games. Nature 448, 1046–1049 (2007). - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

