Impact of autocorrelation on functional connectivity
- PMID: 25072392
- PMCID: PMC4253536
- DOI: 10.1016/j.neuroimage.2014.07.045
Impact of autocorrelation on functional connectivity
Abstract
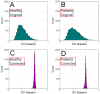
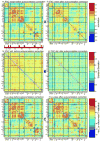
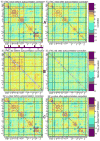
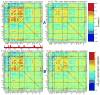
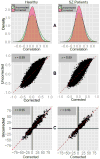
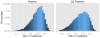
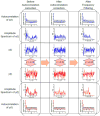
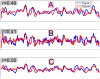
Although the impact of serial correlation (autocorrelation) in residuals of general linear models for fMRI time-series has been studied extensively, the effect of autocorrelation on functional connectivity studies has been largely neglected until recently. Some recent studies based on results from economics have questioned the conventional estimation of functional connectivity and argue that not correcting for autocorrelation in fMRI time-series results in "spurious" correlation coefficients. In this paper, first we assess the effect of autocorrelation on Pearson correlation coefficient through theoretical approximation and simulation. Then we present this effect on real fMRI data. To our knowledge this is the first work comprehensively investigating the effect of autocorrelation on functional connectivity estimates. Our results show that although FC values are altered, even following correction for autocorrelation, results of hypothesis testing on FC values remain very similar to those before correction. In real data we show this is true for main effects and also for group difference testing between healthy controls and schizophrenia patients. We further discuss model order selection in the context of autoregressive processes, effects of frequency filtering and propose a preprocessing pipeline for connectivity studies.
Keywords: Autocorrelation; Autoregressive process; Functional connectivity; Independent component analysis; Resting-state fMRI.
Copyright © 2014 Elsevier Inc. All rights reserved.
Figures



References
-
- Aguirre GK, Zarahn E, D’Esposito M. Empirical analyses of BOLD fMRI statistics. II. Spatially smoothed data collected under null-hypothesis and experimental conditions. Neuroimage. 1997;5:199–212. - PubMed
-
- Akaike H. New Look at Statistical-Model Identification. Ieee Transactions on Automatic Control Ac. 1974;19:716–723.
-
- Allen EA, Erhardt EB, Damaraju E, Gruner W, Segall JM, Silva RF, Havlicek M, Rachakonda S, Fries J, Kalyanam R, Michael AM, Caprihan A, Turner JA, Eichele T, Adelsheim S, Bryan AD, Bustillo J, Clark VP, Feldstein Ewing SW, Filbey F, Ford CC, Hutchison K, Jung RE, Kiehl KA, Kodituwakku P, Komesu YM, Mayer AR, Pearlson GD, Phillips JP, Sadek JR, Stevens M, Teuscher U, Thoma RJ, Calhoun VD. A baseline for the multivariate comparison of resting-state networks. Front Syst Neurosci. 2011;5:2. - PMC - PubMed
-
- Ang AH-S, Tang WH. Probability concepts in engineering planning and design. Wiley; New York: 1975.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

