Computer simulations reveal complex distribution of haemodynamic forces in a mouse retina model of angiogenesis

Abstract

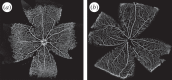
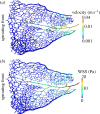
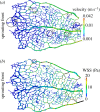
There is currently limited understanding of the role played by haemodynamic forces on the processes governing vascular development. One of many obstacles to be overcome is being able to measure those forces, at the required resolution level, on vessels only a few micrometres thick. In this paper, we present an in silico method for the computation of the haemodynamic forces experienced by murine retinal vasculature (a widely used vascular development animal model) beyond what is measurable experimentally. Our results show that it is possible to reconstruct high-resolution three-dimensional geometrical models directly from samples of retinal vasculature and that the lattice-Boltzmann algorithm can be used to obtain accurate estimates of the haemodynamics in these domains. We generate flow models from samples obtained at postnatal days (P) 5 and 6. Our simulations show important differences between the flow patterns recovered in both cases, including observations of regression occurring in areas where wall shear stress (WSS) gradients exist. We propose two possible mechanisms to account for the observed increase in velocity and WSS between P5 and P6: (i) the measured reduction in typical vessel diameter between both time points and (ii) the reduction in network density triggered by the pruning process. The methodology developed herein is applicable to other biomedical domains where microvasculature can be imaged but experimental flow measurements are unavailable or difficult to obtain.

Keywords: angiogenesis; blood flow; lattice-Boltzmann; mouse; retina; shear stress.

Figure 1.

Murine retinal vascular plexus 6 and 21 days postnatal (panel (a) and (b), respectively). Within days, the primitive vessel network remodels into mature vasculature. Samples were collected, mounted and imaged as described in §3.

Figure 2.

Reported values of murine blood viscosity for different shear rates and Carreau-Yasuda (CY) model fit. (Online version in colour.)

Figure 3.

Hagen–Poiseuille flow in an inclined cylinder. Relative error on the computed flow rate as a function of vessel diameter and lattice-Boltzmann (LB) relaxation time . For , the total error is kept below 3% even for cylinders with just three lattice sites across. These results confirm the suitability of the LB algorithm for the simulation of flow in sparse geometries and porous media. The lines are a guide to the eye and bear no physical meaning. (Online version in colour.)

Figure 4.

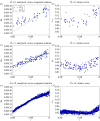
Hagen–Poiseuille shear stress in inclined cylinders of . Norm of the analytical and computed stress tensors (panels 4a,c,e) and relative error between them (panels 4b,d,f). Results are presented for every lattice site with radius . Agreement between computed and analytical solution improves with increasing . These results, with the Bouzidi et al. [50] implementation of the no-slip boundary condition, represent a substantial improvement over the 35% error reported by Stahl et al. [51] with the bounce-back method and . (Online version in colour.)

Figure 5.

Subset of a wild-type P6 retinal plexus used to reconstruct one of our retinal blood flow models, namely P6A model. The original microscope image is segmented and the network skeleton and segment radii are computed. Based on these values, a three-dimensional volume is reconstructed assuming vessels of piecewise constant radius. (a) Original image. (b) Segmented image. (c) Reconstructed surface.

Figure 6.

Binary masks defining the luminal surface of three retinal plexuses obtained at two different stages of development. All plexuses are presented with the area closer to the optic disc at the bottom of the image and the sprouting front at the top. In all samples studied, arteries tend to be thinner and have less daughter vessels than veins. Vessels close to the sprouting front tend to have less well-defined identity with luminal diameters comparable to arteries/veins. This is particularly notable in the P5 samples. Vessel density is also higher close to the sprouting front in P5 retinas.

Figure 7.

Network diameter histogram showing the aggregated total distance covered by vessels of a given diameter. Vertical lines indicate the mode of a lognormal probability distribution fit of each dataset. The values for the models not shown here are 5.51 μm (P5A) and 5.29 μm (P6A). We use these values as an estimate of the typical capillary diameter (the most common type of vessel in the network). Capillaries with diameter approaching 0 μm appear to be undergoing remodelling. Arterial and venular segments present higher diameters ranging up to 34 and 40 μm, respectively. (Online version in colour.)

Figure 8.

P5B simulation results: (a) velocity magnitude plotted on a cross section along the z = 0 plane. Velocity shows the expected parabolic profile across the vessel diameter. Velocity is higher in the artery located at the centre of the domain, in particular close to the optic disc. Velocity magnitude quickly decreases as the artery progresses towards the sprouting front and it stops being a preferential flow path at the points where its identity stops being clearly defined. (b) WSS magnitude plotted on the model surface. Areas of preferential flow tend to experience highest WSS magnitudes. WSS is generally low across the domain except for the arterial segment close to the optic disc and some first-order branches. WSS values higher than 20 Pa are considered unphysiological and the regions experiencing them are coloured in black. Black circles indicate regions of interest referenced in the manuscript.

Figure 9.

P6A simulation results: (a) velocity magnitude plotted on a cross section along the z = 0 plane. Velocity is higher in arteries, veins and segments directly branching from them close to the optic disc. Velocity magnitude is smaller in the sprouting front. However, vessels of preferential flow already exist in the sprouting front; potentially an early indicator of which vessels will survive the pruning process. (b) WSS magnitude plotted on the model surface. Areas of preferential flow tend to experience highest WSS magnitudes. WSS peaks are widely spread across the network. WSS magnitude tends to be lower at the junctions and many vessel segments present a high–low pattern due to local changes in vessel diameter. WSS values higher than 20 Pa are considered unphysiological and the regions experiencing them are coloured in black. Black circles indicate regions of interest referenced in the manuscript.

Figure 10.

Traction vectors (of constant length and coloured according to magnitude) on the luminal surface of the region of interest highlighted in figure 9b. The loop branch undergoing regression (upper branch) experiences a much lower traction magnitude.

Figure 11.

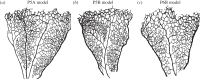
Velocity error residual on simulations with the P6A flow model discretized with Δxⁱ = 1.0, 0.5 and 0.25 μm (diamond-shaped markers). In order to keep the analysis computationally tractable, is computed with results obtained at the lattice sites located on the z = 0 plane only (this is the same subset of the results presented in figure 9). The lines are guides to the eye showing first-order (dashed) and second-order (solid) convergence. (Online version in colour.)

Figure 12.

Simulation results: velocity magnitude plotted on a cross section along the z = 0 plane for OPP values of 45 and 65 mmHg. The logarithmic colour scales have been adjusted to range from 1 mm s⁻¹ to the largest velocity in the domain. Branches of predominant flow and velocity gradients remain fairly constant despite moderate changes in OPP when compared with figure 9a.