Theory of rapid force spectroscopy
- PMID: 25079911
- PMCID: PMC4124868
- DOI: 10.1038/ncomms5463
Theory of rapid force spectroscopy
Abstract
In dynamic force spectroscopy, single (bio-)molecular bonds are actively broken to assess their range and strength. At low loading rates, the experimentally measured statistical distributions of rupture forces can be analysed using Kramers' theory of spontaneous unbinding. The essentially deterministic unbinding events induced by the extreme forces employed to speed up full-scale molecular simulations have been interpreted in mechanical terms, instead. Here we start from a rigorous probabilistic model of bond dynamics to develop a unified systematic theory that provides exact closed-form expressions for the rupture force distributions and mean unbinding forces, for slow and fast loading protocols. Comparing them with Brownian dynamics simulations, we find them to work well also at intermediate pulling forces. This renders them an ideal companion to Bayesian methods of data analysis, yielding an accurate tool for analysing and comparing force spectroscopy data from a wide range of experiments and simulations.
Figures
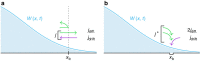
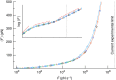
 =10.2 × kBT, xb=1.0 nm, D=1015, nm2 s−1). Squares: ‹F› determined from p(F) (see Methods section), using the fit parameters obtained in Fig. 3. Pentagons: asymptotic analytical approximation equation (40) to ‹F›, using the fit parameters obtained in Fig. 3. Inset shows the same data in double-logarithmic coordinates. The mean rupture force converges onto the Hummer–Szabo asymptote
=10.2 × kBT, xb=1.0 nm, D=1015, nm2 s−1). Squares: ‹F› determined from p(F) (see Methods section), using the fit parameters obtained in Fig. 3. Pentagons: asymptotic analytical approximation equation (40) to ‹F›, using the fit parameters obtained in Fig. 3. Inset shows the same data in double-logarithmic coordinates. The mean rupture force converges onto the Hummer–Szabo asymptote  1/2 at large loading rates,
1/2 at large loading rates,  , and onto the logarithmic DHS asymptote ‹F›~[ln
, and onto the logarithmic DHS asymptote ‹F›~[ln  ]1/2 (ref. 14) at intermediate loading rates,
]1/2 (ref. 14) at intermediate loading rates,  (dashed red lines, shifted upwards for better visibility). In the limit
(dashed red lines, shifted upwards for better visibility). In the limit  →0, external forces are too small to induce rupture, yielding as the measured rupture force the force at the time of spontaneous unbinding, ‹F›~
→0, external forces are too small to induce rupture, yielding as the measured rupture force the force at the time of spontaneous unbinding, ‹F›~ /k0. For our choice of system parameters, the best currently available experimental setup would already be able to access the ballistic regime where ‹F› increases with
/k0. For our choice of system parameters, the best currently available experimental setup would already be able to access the ballistic regime where ‹F› increases with  1/2.
1/2.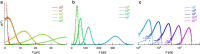
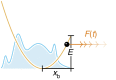
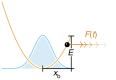
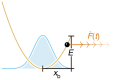
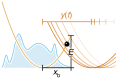
 in our case), apart from a narrow range (b) close to a critical loading rate (
in our case), apart from a narrow range (b) close to a critical loading rate ( c≈105 pN s−1 for our choice of parameters). The ‘experimental’ rupture force histograms have been generated by direct stochastic integration (see Methods section), using
c≈105 pN s−1 for our choice of parameters). The ‘experimental’ rupture force histograms have been generated by direct stochastic integration (see Methods section), using  =10 × kBT, T=300 K, xb=1 nm, D=1,000 nm2 s−1 and
=10 × kBT, T=300 K, xb=1 nm, D=1,000 nm2 s−1 and  =1…1011 pN s−1. Our best-fit parameters obtained with equation (17) are =10.15 × kBT, xb=0.98 nm, D=976 nm2 s−1. Since the mean rupture force varies by orders of magnitude at large loading rates, we use double-logarithmic scaling for
=1…1011 pN s−1. Our best-fit parameters obtained with equation (17) are =10.15 × kBT, xb=0.98 nm, D=976 nm2 s−1. Since the mean rupture force varies by orders of magnitude at large loading rates, we use double-logarithmic scaling for  >107 pN s−1 (c).
>107 pN s−1 (c).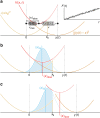

References
-
- Merkel R. Force spectroscopy on single passive biomolecules and single biomolecular bonds. Phys. Rep. 346, 343–385 (2001).
-
- Rief M. & Grubmüller H. Force spectroscopy of single biomolecules. ChemPhysChem 3, 255–261 (2002). - PubMed
-
- Schuler B., Lipman E. A. & Eaton W. A. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature 419, 743–747 (2002). - PubMed
-
- Trepat X., Lenormand G. & Fredberg J. J. Universality in cell mechanics. Soft Matter 4, 1750–1759 (2008).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

