The dynamics of correlated novelties
- PMID: 25080941
- PMCID: PMC5376195
- DOI: 10.1038/srep05890
The dynamics of correlated novelties
Abstract
Novelties are a familiar part of daily life. They are also fundamental to the evolution of biological systems, human society, and technology. By opening new possibilities, one novelty can pave the way for others in a process that Kauffman has called "expanding the adjacent possible". The dynamics of correlated novelties, however, have yet to be quantified empirically or modeled mathematically. Here we propose a simple mathematical model that mimics the process of exploring a physical, biological, or conceptual space that enlarges whenever a novelty occurs. The model, a generalization of Polya's urn, predicts statistical laws for the rate at which novelties happen (Heaps' law) and for the probability distribution on the space explored (Zipf's law), as well as signatures of the process by which one novelty sets the stage for another. We test these predictions on four data sets of human activity: the edit events of Wikipedia pages, the emergence of tags in annotation systems, the sequence of words in texts, and listening to new songs in online music catalogues. By quantifying the dynamics of correlated novelties, our results provide a starting point for a deeper understanding of the adjacent possible and its role in biological, cultural, and technological evolution.
Conflict of interest statement
The authors declare no competing financial interests.
Figures
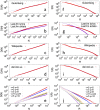
 (see Supplementary Information for the relation of the Heaps' and Zipf's exponents with the model parameters). In all the cases, results for the actual data are compared with two null models, as described in the section Methods.
(see Supplementary Information for the relation of the Heaps' and Zipf's exponents with the model parameters). In all the cases, results for the actual data are compared with two null models, as described in the section Methods.
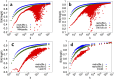
 sequence for a particular label A of the Last.fm dataset. The color code is red for the actual sequence
sequence for a particular label A of the Last.fm dataset. The color code is red for the actual sequence  and blue for the local reshuffle (see methods section) of
and blue for the local reshuffle (see methods section) of  .
.

 is drawn again. In this case one adds this element to
is drawn again. In this case one adds this element to  (depicted at the center of the figure) and, at the same time, puts ρ additional gray balls into
(depicted at the center of the figure) and, at the same time, puts ρ additional gray balls into  . (b) Generic adjacent possible step of the evolution. Here, upon drawing a new ball (red) from
. (b) Generic adjacent possible step of the evolution. Here, upon drawing a new ball (red) from  , ν + 1 brand new balls are added to
, ν + 1 brand new balls are added to  along with the ρ red balls of the reinforcement step that takes place at each time step. (c), (d) Urn model with semantic triggering. Same as above except that now each ball has a label defining its semantic context. The label is conserved during a reinforcement event (e.g., the label A for the gray balls on panel c) while it appears as a brand new label, C, for the ν + 1 balls added for an adjacent possible event (panel d).
along with the ρ red balls of the reinforcement step that takes place at each time step. (c), (d) Urn model with semantic triggering. Same as above except that now each ball has a label defining its semantic context. The label is conserved during a reinforcement event (e.g., the label A for the gray balls on panel c) while it appears as a brand new label, C, for the ν + 1 balls added for an adjacent possible event (panel d).
 in 4 parts and count the occurrences fi of A in each of them (bottom numbers). The normalized entropy of A will be
in 4 parts and count the occurrences fi of A in each of them (bottom numbers). The normalized entropy of A will be  . As a value of S(k) we average all entropies of the elements occurring k-times in
. As a value of S(k) we average all entropies of the elements occurring k-times in  . The numbers at the top show the length of the inter-times used in the interval distribution evaluation. The local reshuffling would shuffle only those 15 elements occurring after the first occurrence of A, and compute the normalized entropy and the time intervals distribution on this reduced sequence.
. The numbers at the top show the length of the inter-times used in the interval distribution evaluation. The local reshuffling would shuffle only those 15 elements occurring after the first occurrence of A, and compute the normalized entropy and the time intervals distribution on this reduced sequence.References
-
- Kauffman S. A. Investigations: The Nature of Autonomous Agents and the Worlds They Mutually Create. SFI working papers (Santa Fe Institute, 1996).
-
- Johnson S. Where Good Ideas Come From: The Natural History of Innovation (Riverhead Hardcover, 2010).
-
- Kauffman S. A. Investigations (Oxford University Press, New York/Oxford, 2000).
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

