PET image reconstruction using kernel method
- PMID: 25095249
- PMCID: PMC4280333
- DOI: 10.1109/TMI.2014.2343916
PET image reconstruction using kernel method
Abstract
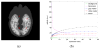
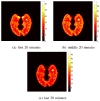
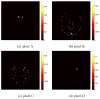
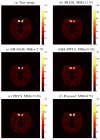
Image reconstruction from low-count positron emission tomography (PET) projection data is challenging because the inverse problem is ill-posed. Prior information can be used to improve image quality. Inspired by the kernel methods in machine learning, this paper proposes a kernel based method that models PET image intensity in each pixel as a function of a set of features obtained from prior information. The kernel-based image model is incorporated into the forward model of PET projection data and the coefficients can be readily estimated by the maximum likelihood (ML) or penalized likelihood image reconstruction. A kernelized expectation-maximization algorithm is presented to obtain the ML estimate. Computer simulations show that the proposed approach can achieve better bias versus variance trade-off and higher contrast recovery for dynamic PET image reconstruction than the conventional maximum likelihood method with and without post-reconstruction denoising. Compared with other regularization-based methods, the kernel method is easier to implement and provides better image quality for low-count data. Application of the proposed kernel method to a 4-D dynamic PET patient dataset showed promising results.
Figures
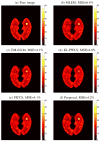
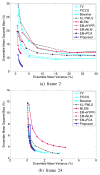
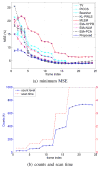
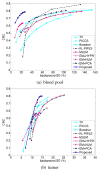

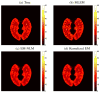

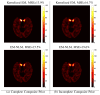
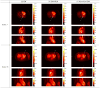

References
-
- Qi J, Leahy RM. Iterative reconstruction techniques in emission computed tomography. Physics in Medicine and Biology. 2006;51(15):R541–R578. - PubMed
-
- Leahy R, Yan X. Incorporation of anatomical MR data for improved functional imaging with PET. Information Processing in Medical Imaging. 1991;(511):105–120. Lecture Notes in Computer Science.
-
- Fessler JA, Clinthorne NH, Rogers WL. Regularized emission image reconstruction using imperfect side information. IEEE Transactions on Nuclear Science. 1992;39(5):1464–1471.
-
- Gindi G, Lee M, Rangarajan A, Zubal IG. Bayesian reconstruction of functional images using anatomical information as priors. IEEE Transactions on Medical Imaging. 1993;12(4):670–680. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

