Bacteria and game theory: the rise and fall of cooperation in spatially heterogeneous environments

Abstract

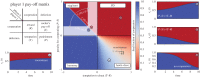
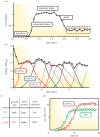
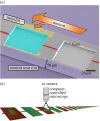
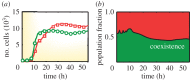
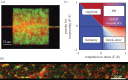
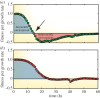
One of the predictions of game theory is that cooperative behaviours are vulnerable to exploitation by selfish individuals, but this result seemingly contradicts the survival of cooperation observed in nature. In this review, we will introduce game theoretical concepts that lead to this conclusion and show how the spatial competition dynamics between microorganisms can be used to model the survival and maintenance of cooperation. In particular, we focus on how Escherichia coli bacteria with a growth advantage in stationary phase (GASP) phenotype maintain a proliferative phenotype when faced with overcrowding to gain a fitness advantage over wild-type populations. We review recent experimental approaches studying the growth dynamics of competing GASP and wild-type strains of E. coli inside interconnected microfabricated habitats and use a game theoretical approach to analyse the observed inter-species interactions. We describe how the use of evolutionary game theory and the ideal free distribution accurately models the spatial distribution of cooperative and selfish individuals in spatially heterogeneous environments. Using bacteria as a model system of cooperative and selfish behaviours may lead to a better understanding of the competition dynamics of other organisms-including tumour-host interactions during cancer development and metastasis.

Keywords: Prisoner's Dilemma; bacteria; game theory.

Figure 1.

Game theory. A pay-off matrix describes the nature of the interactions between two players. Two important variables are the temptation to cheat (T–R), which is the difference between the ‘temptation’ to defect and the ‘reward’ obtained by cooperating, and the penalty incurred by cooperating (P–S), which measures the pay-off when the other player cheats. In the middle panel, equation (2.1) is solved and the final fraction of cooperator x_c(t) as t → ∞ is computed. The colourbar illustrates the value of x_c(∞), the fraction of cooperative individuals within the population at equilibrium, and a few examples of competition between individuals are shown in panels (a–d).

Figure 2.

Evolution under prolonged starvation. (a) Bacterial growth usually begins with a period of quiescence (lag phase), followed by exponential growth, entrance into stationary phase and finally a death phase. During the death phase, more than 99% of the cell population dies as a result of the deteriorating environmental conditions. (b) The small fraction of surviving cells (less than 1%) is not genotypically stable. In this idealized representation, different genotypes arise in succession. Every new genotype is more adapted to stressful conditions than the previous one and usually has mutations conferring a GASP. (d) This table summarizes the properties of the WT and GASP strains. (Adapted from [20,41].) (c) The WT strain grows at a higher rate but will reach a lower density. The GASP cells, on the other hand, grow at a slower pace but reach a higher final density. (Data adapted from [20].)

Figure 3.

Micro-habitat patch device. (Adapted from [15].) (a) We physically recreate a metapopulation landscape using microfabrication. Each chamber is 100 × 100 × 10 µm in size (highlighted in cyan), and the 200 nm nanoslits (yellow) are deep enough to allow nutrients to freely diffuse inside the MHPs but small enough to prevent cells from migrating into the nutrient reservoirs. Cells can migrate between each micro-habitat using the 5 µm wide junction channels (red). (b) A computer-controlled microscope records the fluorescence intensity in each chamber every 15 min.

Figure 4.

Growth dynamics under competition. (Adapted from [20].) (a) Growth of competing WT and GASP mutant populations (green, WT; red, GASP) in the nutrient-rich regions. (b) The time evolution of the population fraction in the nutrient-rich region shows that cells coexist at an approximately equal fraction inside the device.

Figure 5.

Long-range spatial correlation. (a) Kymograph representation of the dynamics of the WT (green) and GASP (red) populations within the device. (b) Kimura & Weiss's average intra-species spatial correlation between neighbouring habitats as a function of distance is extracted from the fluorescence levels in each MHP. We find that the correlation length for the WT population (green circles) is longer than that of the GASP population (red squares).

Figure 6.

Spatial coexistence. (a,b) WT and GASP cells are able to coexist spatially in each MHP at different scales. (Adapted from [16,18].) (c) WT and GASP cells were shown to interact according to a PD type of game [22], which would inevitably lead to the extinction of the WT population under well-stirred conditions. The observation that cooperator and defector populations can coexist in a spatial PD game suggests that the phase diagram describing spatial competition must be modified to account for the observed spatial coexistence.

Figure 7.

Heterogeneous fitness landscape—WT control. Correlation coefficient between nutrient access (number of nanoslits) and the cell density. Any value higher than 0.5 indicates ‘strong’ correlations. Inset: number of nanoslits open versus position.

Figure 8.

Heterogeneous fitness landscape. The final density of WT and GASP mutant cells strongly depends on the coupling between the nutrient reservoirs and the MHP array. Here, WT cells perform better in regions where the coupling is weak (less than two nanoslits), whereas GASP mutants perform better in regions where the coupling is strong (more than five nanoslits).

Figure 9.

Growth and population distribution. (Adapted from [15].) (a) An example of two neighbouring patches where an anomalous distribution of GASP and WT cells is observed. (b,c) The fraction and overall growth of WT and GASP cells in the nutrient-rich regions show that the WT population leaves the nutrient-rich environments as the density of GASP mutants increases. (d,e) Comparatively, the fraction and overall growth of WT cells is higher in the nutrient-poor regions.

Figure 10.

Large-scale periodic fitness landscape. In environments where the fitness landscape varies on larger spatial scales, we observe similar dynamics: WT cells initially populate nutrient-rich regions but are dislodged by GASP cells following their entrance into stationary phase.

Figure 11.

Conditioned medium experiments. Experiments where the nutrient reservoirs contain conditioned medium (i.e. growth medium partially depleted of nutrients) are performed. (a) While GASP cells dominate in both the nutrient-rich and (b) the nutrient-poor habitats, the WT population does not go extinct and stable levels are maintained in both environments.

Figure 12.

Measured fitness of WT cells over time. (Adapted from [15].) (a) The fitness of WT cells decreases below 0 (at T = 15 h, indicated by the arrow). This occurs as the combined density of WT and GASP cells is higher than the carrying capacity of the WT species alone. (b) The fitness of the GASP population inside the nutrient-rich regions remains positive throughout the experiment.

Figure 13.

The IFD under conditioned medium experiments. (a) Large-scale competition dynamics show that while WT cells still survive in the presence of selfish GASP cells, their final density is severely affected by the deteriorated environmental conditions. (b) The computed fitness of the WT cells decreases and stays below 0 much more rapidly than in the nutrient-rich experiment (fitness becomes negative at T = 9 h compared with T = 15 h in fresh medium).