Combating unmeasured confounding in cross-sectional studies: evaluating instrumental-variable and Heckman selection models

Abstract

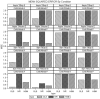
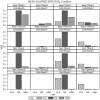
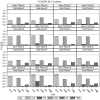
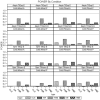
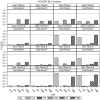
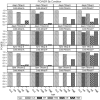
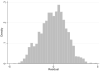
Unmeasured confounding is the principal threat to unbiased estimation of treatment "effects" (i.e., regression parameters for binary regressors) in nonexperimental research. It refers to unmeasured characteristics of individuals that lead them both to be in a particular "treatment" category and to register higher or lower values than others on a response variable. In this article, I introduce readers to 2 econometric techniques designed to control the problem, with a particular emphasis on the Heckman selection model (HSM). Both techniques can be used with only cross-sectional data. Using a Monte Carlo experiment, I compare the performance of instrumental-variable regression (IVR) and HSM to that of ordinary least squares (OLS) under conditions with treatment and unmeasured confounding both present and absent. I find HSM generally to outperform IVR with respect to mean-square-error of treatment estimates, as well as power for detecting either a treatment effect or unobserved confounding. However, both HSM and IVR require a large sample to be fully effective. The use of HSM and IVR in tandem with OLS to untangle unobserved confounding bias in cross-sectional data is further demonstrated with an empirical application. Using data from the 2006-2010 General Social Survey (National Opinion Research Center, 2014), I examine the association between being married and subjective well-being.

Figure 1

Unmeasured confounding in cross-sectional data.

Figure 2

Simulation results for N = 50 with treatment effect present. Sym T = symmetric treatment condition; Asym T = asymmetric treatment condition; Norm E = normal errors; Exp E = exponential errors; Cnfd P = confound present; Cnfd A = confound absent; Inst P = instrument present; Inst A = instrument absent; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model.

Figure 3

Simulation results for N = 250 with treatment effect present. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition; Norm E = normal errors; Exp E = exponential errors; Cnfd P = confound present; Cnfd A = confound absent; Inst P = instrument present; Inst A = instrument absent; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model.

Figure 4

Simulation results for N = 2,000 with treatment effect present. Sym T = symmetric treatment condition; Asym T = asymmetric treatment condition; Norm E = normal errors; Exp E = exponential errors; Cnfd P = confound present; Cnfd A = confound absent; Inst P = instrument present; Inst A = instrument absent; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model.

Figure 5

Simulation results for N = 50 with treatment effect present. Sym T = symmetric treatment condition; Asym T = asymmetric treatment condition; Norm E = normal errors; Exp E = exponential errors; Cnfd P = confound present; Cnfd A = confound absent; Inst P = instrument present; Inst A = instrument absent; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 6

Simulation results for N = 50 with treatment effect absent. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error, OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 7

Simulation results for N = 250 with treatment effect present. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 8

Simulation results for N = 250 with treatment effect absent. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 9

Simulation results for N = 2,000 with treatment effect present. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 10

Simulation results for N = 2,000 with treatment effect absent. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 11

Residuals from ordinary least squares (OLS) regression of life distress on model predictors.