Learning a weighted meta-sample based parameter free sparse representation classification for microarray data

Abstract

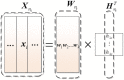
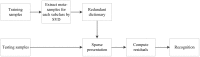
Sparse representation classification (SRC) is one of the most promising classification methods for supervised learning. This method can effectively exploit discriminating information by introducing a [Symbol: see text]1 regularization terms to the data. With the desirable property of sparisty, SRC is robust to both noise and outliers. In this study, we propose a weighted meta-sample based non-parametric sparse representation classification method for the accurate identification of tumor subtype. The proposed method includes three steps. First, we extract the weighted meta-samples for each sub class from raw data, and the rationality of the weighting strategy is proven mathematically. Second, sparse representation coefficients can be obtained by [Symnbol: see text]1 regularization of underdetermined linear equations. Thus, data dependent sparsity can be adaptively tuned. A simple characteristic function is eventually utilized to achieve classification. Asymptotic time complexity analysis is applied to our method. Compared with some state-of-the-art classifiers, the proposed method has lower time complexity and more flexibility. Experiments on eight samples of publicly available gene expression profile data show the effectiveness of the proposed method.

Figure 1. Illustration of meta-sample model: each column vector of can be represented within a linear combination of meta-samples in , and the column of corresponds to the linear combination coefficients.

Figure 2. Optimal classification accuracy of MSRC achieved on COLON; the -axis represents the number of meta-samples (left) and the regularization parameter (right).

Classification accuracy is more sensitive to the number of meta-samples rather than to the regularization parameter.

Figure 3. The flowchart of PFMSRC scheme.

Figure 4. Comparison of prediction accuracy on four binary classification datasets by varying the number of samples from per subclass; when is larger than 10 the model based method prediction accuracy decreases as increases.

Figure 5. Comparison of prediction accuracy on four multiclass classification datasets by varying the number of samples from per subclass; when is larger than 10 the performance degradation of model based methods is less significant than that of binary classification.

Figure 6. Comparison of prediction accuracy on four binary classification datasets by varying the number of top selected genes.

Figure 7. Comparison of prediction accuracy on four multiclass classification datasets by varying the number of top selected genes.