Network structure within the cerebellar input layer enables lossless sparse encoding

Abstract

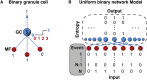
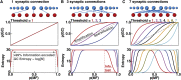
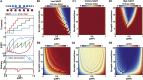
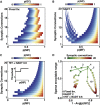
The synaptic connectivity within neuronal networks is thought to determine the information processing they perform, yet network structure-function relationships remain poorly understood. By combining quantitative anatomy of the cerebellar input layer and information theoretic analysis of network models, we investigated how synaptic connectivity affects information transmission and processing. Simplified binary models revealed that the synaptic connectivity within feedforward networks determines the trade-off between information transmission and sparse encoding. Networks with few synaptic connections per neuron and network-activity-dependent threshold were optimal for lossless sparse encoding over the widest range of input activities. Biologically detailed spiking network models with experimentally constrained synaptic conductances and inhibition confirmed our analytical predictions. Our results establish that the synaptic connectivity within the cerebellar input layer enables efficient lossless sparse encoding. Moreover, they provide a functional explanation for why granule cells have approximately four dendrites, a feature that has been evolutionarily conserved since the appearance of fish.

Figure 1

Granule Cell and Glomerular Density in the Rat Cerebellum and Construction of a Local Granule Cell Layer Model (A) Measurements performed in lobule VIa (red area) of a parasagittal slice of cerebellar vermis. (B) Regions of granule cell layer (GCL) with pairs of sections (left and right) and frames used for the unbiased counting method (cells on green edges are counted and on red edges excluded). (C–E) Area of GCL immunolabeled for Kv4.2 (C) showing circular GC somatic outlines, VGAT (D), and VGLUT1 (E). (F) Overlay of immunolabels for Kv4.2 (red), VGAT (green), and VGLUT1 (blue). (G) Colabeling of the three markers used to demarcate a glomerulus. (H) 3D anatomically constrained model of the local GCL network, consisting of a 40-μm-radius ball of glomeruli (red) and GCs (blue) with four dendrites per GC (black lines). (I) Distribution of GC dendrite length in the local GCL network model. (J) Distribution of the number of GC dendrites per MF rosette. (C)–(F) are at the same magnification, with scale bar on (F) applying to all panels. Scales, 1 mm in (A), 20 μm in (B)–(F), and 2 μm in G.

Figure 2

Schematic Representation of the Uniform Binary Network Model (A) Schematic diagram showing binary mossy fiber (MF) synaptic inputs (red) and a linear thresholding binary granule cell (GC, blue) with a single MF synaptic connection per dendrite (blue lines). GC output is 1 if the sum of its MF input values is equal to the threshold or greater and 0 otherwise. (B) Uniform binary network model is a random bipartite graph consisting of binary MFs and linear threshold GC units. Network with 3 MF synaptic connections per GC (d = 3), shown only for the three central GCs for clarity. N events, encoded as binary MF input patterns, are transformed into a binary GC output patterns. GC population entropy is calculated from the distribution of output patterns.

Figure 3

Number of Synaptic Connections per Neuron and Threshold Determine the Transmission and Transformation of Information in a Uniform Binary Network Model (A) Top: schematic illustration of mossy fibers (MF, red) and granule cells (GCs) (blue) for a binary network with one MF synaptic connection per GC (d = 1; blue lines, shown for 3 GCs only). Middle: GC activation probability (p(GC)) as a function of MF activation probability (p(MF)), red line for a threshold of 1. Gray dashed line indicates p(GC) = p(MF). Bottom: information (entropy) in GC population as a function of p(MF) for one billion events. Vertical dashed lines indicate range of p(MF) where >99% of the information is encoded by the GC population. (B) Same as for (A) but for a network with d = 3 and all possible threshold values (1-3 red-blue). (C) Same as for (B) but for d = 7 (1-7 red-cyan).

Figure 4

Effect of Synaptic Connectivity on Information Transmission and Population Activity in Uniform Binary Network Models with a Fixed Relative Threshold (A) Quantity of event information (entropy) encoded by the granule cell (GC) population across the full range of mossy fiber (MF) activation probability p(MF) for uniform binary network models with different numbers of synaptic connections per GC (d) and a fixed relative threshold φ = ceiling [0.75 × d]. (B) GC activation probability p(GC) for the same network configurations as in (A). (C) Same as for (B) but visualized as a line plot to show the relationship between p(GC) and p(MF) for different models. (D) From left to right: a sample of 400 MF input patterns (events) with p(MF) = 0.3, where active MFs are red and inactive MFs are white, schematic network representation and GC output activity patterns (blue raster plot) for a network with d = 3 (see label D in panels A and B). Bar graph indicates p(GC) and entropy for one billion patterns, as for (A). (E) Same as for (D) but for d = 20 (see label E in panels A and B). (F) Same as for (D) but for d = 20 and p(MF) = 0.8 (see label F in panels A and B).

Figure 5

Effect of Activity-Dependent Threshold Regulation on the Trade-Off between Information Transmission and Sparsification (A) Top: uniform binary network model schematic with mossy fibers (MFs) in red and granule cells (GCs) in blue (top); GC network-activity-dependent threshold (NADT) for low (0.5, blue), unity (1.0, green), and high (2.0, red) NADT, for a network with seven synaptic connections per GC (d = 7; connections for center 3 GCs shown for clarity). Middle: GC activation probability (p(GC)) versus MF activation probability (p(MF)) for the NADT functions above. Bottom: information encoded by GCs for each threshold function. (B1 and B2) Information encoded by GCs and p(GC), respectively, for low NADT networks with different d. (C1 and C2 and D1 and D2) Same as for (B1 and B2) for unity NADT and high NADT, respectively.

Figure 6

Networks that Best Perform Lossless Sparse Encoding Have Few Synaptic Connections per Neuron (A) Granule cell activation probability (p(GC)) versus mossy fiber activation probability (p(MF)) with different numbers of synaptic connections per GC (d) for a fixed relative threshold (φ = ceiling[0.75 × d]). Colored regions indicate sparse encodable range, where >99% of information was encoded and p(GC) < p(MF). (B and C) Same as for (A) but for network-activity-dependent threshold (NADT) = 2 and a high initial threshold (HIT) combined with NADT = 0.6, respectively. Inset in (C) shows threshold function for networks with d = 4. (D) Relationship between size of sparse encodable range and output sparseness (1-Avg[p(GC)] averaged across all values of p(MF)). Color code indicates d and circle, square, and triangle symbols show different threshold functions in (A), (B), and (C), respectively.

Figure 7

Construction and Analysis of an Experimentally Constrained Spiking Model of the Local Granule Cell Layer Network Incorporating Synaptic Mechanisms and Tonic Inhibition (A) Excitatory AMPAR (red) and NMDAR (purple) synaptic conductances for four independent mossy fiber (MF) inputs injected into a model granule cell (GC). Top two traces: active MFs with excitatory conductance driven by independent Poisson spike trains firing at 80 Hz. Lower two traces: inactive MF firing at 10 Hz. Bottom trace: tonic inhibitory GABA_AR conductance (green). (B) Model GC with action potential firing rate-coded input-output relationship (above) for four synaptic inputs. (C) Membrane potential of model GC during synaptic input in (A). (D) Fit of the short-term plasticity model (red) of the AMPAR component to an experimental recording of a 100 Hz synaptic conductance train (gray). (E) Same as for (D) but for the NMDAR component and an 80 Hz conductance train. Inset: voltage dependence of NMDAR conductance. (F) A binary stimulus pattern was randomly selected from a set of N patterns (black active and white inactive on barcode). A Poisson spike train was generated for each MF input (80 Hz active, 10 Hz inactive; red raster plot), thereby setting the timing of synaptic conductances (as in A). Red barcode indicates spike counts for the given realization of the spike trains. (G) 3D view of the anatomically constrained local GCL network model with 176 MFs in red and 509 GCs in blue. (H) Raster plot of GC firing activity in response to the input. Blue barcode indicates GC spike count vector (measured over a 30 ms window), which was assigned to one of N output classes (black bar codes) defined using the k-means algorithm on a separate data set.

Figure 8

Sparse Encoding in Biologically Detailed Spiking Network Models with Different Numbers of Synaptic Connections per Granule Cell (A) Visualization of independent mossy fiber (MF) inputs in the local granule cell (GC) layer network model with active MFs in red and inactive MFs in white, for an example random activation pattern. (B) Mutual information (MI) encoded by the GC population for 1,024 uncorrelated input patterns across the full range of MF activation probability p(MF) in biologically detailed spiking networks with different numbers of synaptic connections per GC (d). (C) Same as for (B) but for 1-average output sparseness (analogous to p(GC) in UBN model). (D, E, and F) Same as for (A), (B), and (C) but for a set of 1,024 spatially correlated patterns, where neighboring MF inputs were activated in groups of five. (G) Same as for (B) and (E) but visualized as a line plot to show the relationship between average spikes per GC and average spikes per MF in a 30 ms window across all values of p(MF), for networks with different d. (H) Relationship between average MI (normalized by the MF input entropy) and average output sparseness (across all values of p(MF)) for spiking networks with different d (color code) for independent (circles) and spatially correlated (triangles) inputs.