A memory of errors in sensorimotor learning
- PMID: 25123484
- PMCID: PMC4506639
- DOI: 10.1126/science.1253138
A memory of errors in sensorimotor learning
Abstract
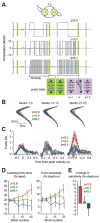
The current view of motor learning suggests that when we revisit a task, the brain recalls the motor commands it previously learned. In this view, motor memory is a memory of motor commands, acquired through trial-and-error and reinforcement. Here we show that the brain controls how much it is willing to learn from the current error through a principled mechanism that depends on the history of past errors. This suggests that the brain stores a previously unknown form of memory, a memory of errors. A mathematical formulation of this idea provides insights into a host of puzzling experimental data, including savings and meta-learning, demonstrating that when we are better at a motor task, it is partly because the brain recognizes the errors it experienced before.
Copyright © 2014, American Association for the Advancement of Science.
Figures


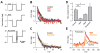
References
-
- Jordan MI, Rumelhart DE. Forward Models - Supervised Learning with a Distal Teacher. Cognitive Science. 1992 Jul-Sep;16:307.
-
- Kawato M, Furukawa K, Suzuki R. A Hierarchical Neural-Network Model for Control and Learning of Voluntary Movement. Biological cybernetics. 1987;57:169. - PubMed
-
- Robinson FR, Noto CT, Bevans SE. Effect of visual error size on saccade adaptation in monkey. J Neurophysiol. 2003 Aug;90:1235. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

