Equilibrium Conformations of Concentric-tube Continuum Robots

Abstract

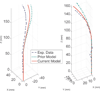
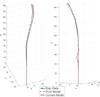
Robots consisting of several concentric, preshaped, elastic tubes can work dexterously in narrow, constrained, and/or winding spaces, as are commonly found in minimally invasive surgery. Previous models of these "active cannulas" assume piecewise constant precurvature of component tubes and neglect torsion in curved sections of the device. In this paper we develop a new coordinate-free energy formulation that accounts for general preshaping of an arbitrary number of component tubes, and which explicitly includes both bending and torsion throughout the device. We show that previously reported models are special cases of our formulation, and then explore in detail the implications of torsional flexibility for the special case of two tubes. Experiments demonstrate that this framework is more descriptive of physical prototype behavior than previous models; it reduces model prediction error by 82% over the calibrated bending-only model, and 17% over the calibrated transmissional torsion model in a set of experiments.

Keywords: active cannula; concentric tube robot; continuum robot; elastica; flexible arms; kinematics; mechanics; medical robots; snake-like robot; variational calculus.

Fig. 1

A prototype active cannula made of four superelastic Nitinol tubes and one central wire (with three tubes and the wire visible).

Fig. 2

The coordinate frames for the first and the ith tubes at an arbitrary cross section of the active cannula. They differ by an angular rotation of θ about their z-axes, which are both tangent to the curve. The curvatures, ω and ω_i, of the frames are not pictured, since they may in general lie in any direction with respect to the coordinate frames.

Fig. 3

Simulation of the tubes given in Table 1 with the inner wire rotated to a base angle of α₁ = −180° so that θ₀ = 180°. Three equilibrium conformations are shown corresponding to the three boundary condition solutions shown in Figure 4. The solution with θ_L2 = 84.4° is reached by rotating α₁ in the negative direction to α₁ = −180°, and the solution θ_L2 = 275.6° is be reached by rotating α₁ in the positive direction to α₁ = 180°. The solution with θ_L = 180° is the trivial (unstable) solution, with the tubes undergoing no torsion.

Fig. 4

Plot of the left-hand side of Equation (43) versus θ_L for the tubes in Table 1 and θ₀ = 180°. Solutions for θ_L satisfying (43) are shown at θ_L = 180°, θ_L = 84.4°, and θ_L = 275.6°.

Fig. 5

For θ₀ = 180° the value of the integral in (44) is shown in blue as a function of θ_L ranging from 0° to 360°. Because it is lower bounded by π/2, the dimensionless parameter $L\sqrt{a}$ can be used to predict when multiple solutions can occur.

Fig. 6

Four configurations of a simulation of two fully precurved, fully overlapping tubes, whose material properties are given in Table 1. Both tubes have a longer arc length of 636.5 mm (equal to one full circle of the outer tube). The inner wire is rotated in the positive direction to angles of 90°, 225°, 315°, and 350° at the base. It is evident that in extreme cases, circular tubes with precurvature can form highly non-circular shapes when combined due to the effects of torsion.

Fig. 7

Diagram of tube overlap configuration with variables from (46) shown.

Fig. 8

Manual actuation mechanism used in the experiments. In this apparatus, both tube and wire are affixed to circular acrylic input handles at their bases, which are etched to encode rotation. The support structure is etched with a linear ruler to encode translation. Spring pin locking mechanisms lock the input disks at desired linear and angular input positions. The inset image of a striped cannula on a white background is an example of an image captured using one of our calibrated stereo cameras. The black bands seen are electrical tape and allow for point correspondences to be identified for stereo triangulation. The red circles indicate the locations at which Euclidean errors were calculated. Calibration of model parameters was done to minimize the sum of these errors over all experiments.

Fig. 9

Configuration space covered in experiments. Left: partial overlap case. Right: full overlap case.

Fig. 10

Comparison of shape for the transmissional torsion model (green – dotted line) with nominal parameters, the model given in Section 4 (red – solid line) with nominal parameters, and experimental data (blue – dashed line) for configurations near the edge of the active cannula workspace. Note that the model given in Section 4 produces predictions closer to experimentally observed cannula shape. Left: partial overlap case. Right: full overlap case.

Fig. 11

Comparison of shape for the transmissional torsion model (green – dotted line) with calibrated parameters, the model given in Section 4 (red – solid line) with calibrated parameters, and experimental data (blue – dashed line) for configurations near the edge of the active cannula workspace. Note that the model given in Section 4 produces predictions closer to experimentally observed cannula shape. Left: partial overlap case. Right: full overlap case.

Fig. 12

Error versus arc length for the 200° partial overlap case with nominal parameter values using the model of Section 4. The general increase in error from base to tip is characteristic of all experiments, and thus tip error provides a reasonable metric for our experimental dataset.

Fig. 13

Angle ϕ of that defines the resulting instantaneous plane of curvature of the active cannula. Left: partial overlap case. Right: full overlap case.