Gyrification from constrained cortical expansion
- PMID: 25136099
- PMCID: PMC4156754
- DOI: 10.1073/pnas.1406015111
Gyrification from constrained cortical expansion
Abstract
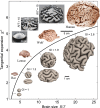
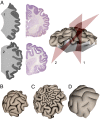
The exterior of the mammalian brain--the cerebral cortex--has a conserved layered structure whose thickness varies little across species. However, selection pressures over evolutionary time scales have led to cortices that have a large surface area to volume ratio in some organisms, with the result that the brain is strongly convoluted into sulci and gyri. Here we show that the gyrification can arise as a nonlinear consequence of a simple mechanical instability driven by tangential expansion of the gray matter constrained by the white matter. A physical mimic of the process using a layered swelling gel captures the essence of the mechanism, and numerical simulations of the brain treated as a soft solid lead to the formation of cusped sulci and smooth gyri similar to those in the brain. The resulting gyrification patterns are a function of relative cortical expansion and relative thickness (compared with brain size), and are consistent with observations of a wide range of brains, ranging from smooth to highly convoluted. Furthermore, this dependence on two simple geometric parameters that characterize the brain also allows us to qualitatively explain how variations in these parameters lead to anatomical anomalies in such situations as polymicrogyria, pachygyria, and lissencephalia.
Keywords: brain morphogenesis; elastic instability.
Conflict of interest statement
The authors declare no conflict of interest.
Figures




References
-
- Striedter GF. Principles of Brain Evolution. Sunderland, MA: Sinauer Associates; 2005.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

