Computing the Free Energy Barriers for Less by Sampling with a Coarse Reference Potential while Retaining Accuracy of the Target Fine Model
- PMID: 25136268
- PMCID: PMC4132848
- DOI: 10.1021/ct500109m
Computing the Free Energy Barriers for Less by Sampling with a Coarse Reference Potential while Retaining Accuracy of the Target Fine Model
Abstract
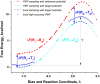
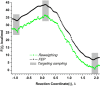
Proposed in this contribution is a protocol for calculating fine-physics (e.g., ab initio QM/MM) free-energy surfaces at a high level of accuracy locally (e.g., only at reactants and at the transition state for computing the activation barrier) from targeted fine-physics sampling and extensive exploratory coarse-physics sampling. The full free-energy surface is still computed but at a lower level of accuracy from coarse-physics sampling. The method is analytically derived in terms of the umbrella sampling and the free-energy perturbation methods which are combined with the thermodynamic cycle and the targeted sampling strategy of the paradynamics approach. The algorithm starts by computing low-accuracy fine-physics free-energy surfaces from the coarse-physics sampling in order to identify the reaction path and to select regions for targeted sampling. Thus, the algorithm does not rely on the coarse-physics minimum free-energy reaction path. Next, segments of high-accuracy free-energy surface are computed locally at selected regions from the targeted fine-physics sampling and are positioned relative to the coarse-physics free-energy shifts. The positioning is done by averaging the free-energy perturbations computed with multistep linear response approximation method. This method is analytically shown to provide results of the thermodynamic integration and the free-energy interpolation methods, while being extremely simple in implementation. Incorporating the metadynamics sampling to the algorithm is also briefly outlined. The application is demonstrated by calculating the B3LYP//6-31G*/MM free-energy barrier for an enzymatic reaction using a semiempirical PM6/MM reference potential. These modifications allow computing the activation free energies at a significantly reduced computational cost but at the same level of accuracy compared to computing full potential of mean force.
Figures





Similar articles
-
Quantum mechanics/molecular mechanics minimum free-energy path for accurate reaction energetics in solution and enzymes: sequential sampling and optimization on the potential of mean force surface.J Chem Phys. 2008 Jan 21;128(3):034105. doi: 10.1063/1.2816557. J Chem Phys. 2008. PMID: 18205486
-
Paradynamics: an effective and reliable model for ab initio QM/MM free-energy calculations and related tasks.J Phys Chem B. 2011 Jun 23;115(24):7950-62. doi: 10.1021/jp201217b. Epub 2011 May 27. J Phys Chem B. 2011. PMID: 21618985 Free PMC article.
-
Multireference Generalization of the Weighted Thermodynamic Perturbation Method.J Phys Chem A. 2022 Nov 17;126(45):8519-8533. doi: 10.1021/acs.jpca.2c06201. Epub 2022 Oct 27. J Phys Chem A. 2022. PMID: 36301936 Free PMC article.
-
Biomolecular force fields: where have we been, where are we now, where do we need to go and how do we get there?J Comput Aided Mol Des. 2019 Feb;33(2):133-203. doi: 10.1007/s10822-018-0111-4. Epub 2018 Nov 30. J Comput Aided Mol Des. 2019. PMID: 30506158 Review.
-
Taming Rugged Free Energy Landscapes Using an Average Force.Acc Chem Res. 2019 Nov 19;52(11):3254-3264. doi: 10.1021/acs.accounts.9b00473. Epub 2019 Nov 4. Acc Chem Res. 2019. PMID: 31680510 Review.
Cited by
-
Enhancing Paradynamics for QM/MM Sampling of Enzymatic Reactions.J Phys Chem B. 2016 Mar 10;120(9):2155-64. doi: 10.1021/acs.jpcb.5b11966. Epub 2016 Feb 29. J Phys Chem B. 2016. PMID: 26866994 Free PMC article.
-
QM/MM free energy simulations: recent progress and challenges.Mol Simul. 2016;42(13):1056-1078. doi: 10.1080/08927022.2015.1132317. Epub 2016 Jul 5. Mol Simul. 2016. PMID: 27563170 Free PMC article.
-
Ambient-Potential Composite Ewald Method for ab Initio Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation.J Chem Theory Comput. 2016 Jun 14;12(6):2611-32. doi: 10.1021/acs.jctc.6b00198. Epub 2016 May 26. J Chem Theory Comput. 2016. PMID: 27171914 Free PMC article.
-
Recent advances in QM/MM free energy calculations using reference potentials.Biochim Biophys Acta. 2015 May;1850(5):954-965. doi: 10.1016/j.bbagen.2014.07.008. Epub 2014 Jul 16. Biochim Biophys Acta. 2015. PMID: 25038480 Free PMC article. Review.
References
-
- Luzhkov V.; Warshel A. Microscopic models for quantum mechanical calculations of chemical processes in solutions: LD/AMPAC and SCAAS/AMPAC calculations of solvation energies. J. Comput. Chem. 1992, 13, 199.
- Bentzien J.; Muller R. P.; Florián J.; Warshel A. Hybrid ab initio quantum mechanics/molecular mechanics calculations of free-energy surfaces for enzymatic reactions: The nucleophilic attack in subtilisin. J. Phys. Chem. B 1998, 102122293.
- Muller R. P.; Warshel A. Ab initio calculations of free-energy barriers for chemical reactions in solution. J. Phys. Chem. 1995, 99, 17516. - PubMed
- Rosta E.; Klahn M.; Warshel A. Towards accurate ab initio QM/MM calculations of free-energy profiles of enzymatic reactions. J. Phys. Chem. B 2006, 11062934. - PubMed
- Polyak I.; Benighaus T.; Boulanger E.; Thiel W. Quantum mechanics/molecular mechanics dual Hamiltonian free-energy perturbation. J. Chem. Phys. 2013, 1396064105. - PubMed
- Claeyssens F.; Harvey J. N.; Manby F. R.; Mata R. A.; Mulholland A. J.; Ranaghan K. E.; Schutz M.; Thiel S.; Thiel W.; Werner H. J. High-accuracy computation of reaction barriers in enzymes. Angew. Chem., Int. Ed. 2006, 45416856. - PubMed
- Rod T. H.; Ryde U. Quantum mechanical free-energy barrier for an enzymatic reaction. Phys. Rev. Lett. 2005, 9413138302. - PubMed
- Hou G.; Cui Q. Stabilization of different types of transition states in a single enzyme active site: QM/MM analysis of enzymes in the alkaline phosphatase superfamily. J. Am. Chem. Soc. 2013, 1352810457. - PMC - PubMed
-
- Heimdal J.; Ryde U. Convergence of QM/MM free-energy perturbations based on molecular-mechanics or semiempirical simulations. Phys. Chem. Chem. Phys. 2012, 143612592. - PubMed
- Plotnikov N. V.; Warshel A. Exploring, refining, and validating the paradynamics QM/MM sampling. J. Phys. Chem. B 2012, 1163410342. - PubMed
-
- Torrie G. M.; Valleau J. P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 232187.
-
- Shirts M. R.; Mobley D. L.; Chodera J. D.; Pande V. S. Accurate and efficient corrections for missing dispersion interactions in molecular simulations. J. Phys. Chem. B 2007, 1114513052. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
