Geometry regulates traction stresses in adherent cells
- PMID: 25140417
- PMCID: PMC4142236
- DOI: 10.1016/j.bpj.2014.06.045
Geometry regulates traction stresses in adherent cells
Abstract
Cells generate mechanical stresses via the action of myosin motors on the actin cytoskeleton. Although the molecular origin of force generation is well understood, we currently lack an understanding of the regulation of force transmission at cellular length scales. Here, using 3T3 fibroblasts, we experimentally decouple the effects of substrate stiffness, focal adhesion density, and cell morphology to show that the total amount of work a cell does against the substrate to which it is adhered is regulated by the cell spread area alone. Surprisingly, the number of focal adhesions and the substrate stiffness have little effect on regulating the work done on the substrate by the cell. For a given spread area, the local curvature along the cell edge regulates the distribution and magnitude of traction stresses to maintain a constant strain energy. A physical model of the adherent cell as a contractile gel under a uniform boundary tension and mechanically coupled to an elastic substrate quantitatively captures the spatial distribution and magnitude of traction stresses. With a single choice of parameters, this model accurately predicts the cell's mechanical output over a wide range of cell geometries.
Copyright © 2014 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures
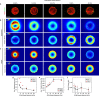
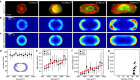
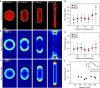
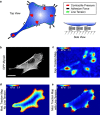
Comment in
-
Work and tension: new evidence that adherent cells of the same area do the same work independent of stiffness and focal adhesions.Biophys J. 2014 Aug 19;107(4):798-9. doi: 10.1016/j.bpj.2014.07.003. Biophys J. 2014. PMID: 25140413 Free PMC article. No abstract available.
References
-
- Lecuit T., Lenne P.-F. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat. Rev. Mol. Cell Biol. 2007;8:633–644. - PubMed
-
- Gupton S.L., Waterman-Storer C.M. Spatiotemporal feedback between actomyosin and focal-adhesion systems optimizes rapid cell migration. Cell. 2006;125:1361–1374. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

