Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Nov;25(6):889-97.
doi: 10.1097/EDE.0000000000000160.

The parametric g-formula for time-to-event data: intuition and a worked example

Alexander P Keil  1 , Jessie K Edwards, David B Richardson, Ashley I Naimi, Stephen R Cole
Affiliations

The parametric g-formula for time-to-event data: intuition and a worked example

Alexander P Keil et al. Epidemiology. 2014 Nov.

Abstract

Background: The parametric g-formula can be used to estimate the effect of a policy, intervention, or treatment. Unlike standard regression approaches, the parametric g-formula can be used to adjust for time-varying confounders that are affected by prior exposures. To date, there are few published examples in which the method has been applied.

Methods: We provide a simple introduction to the parametric g-formula and illustrate its application in an analysis of a small cohort study of bone marrow transplant patients in which the effect of treatment on mortality is subject to time-varying confounding.

Results: Standard regression adjustment yields a biased estimate of the effect of treatment on mortality relative to the estimate obtained by the g-formula.

Conclusions: The g-formula allows estimation of a relevant parameter for public health officials: the change in the hazard of mortality under a hypothetical intervention, such as reduction of exposure to a harmful agent or introduction of a beneficial new treatment. We present a simple approach to implement the parametric g-formula that is sufficiently general to allow easy adaptation to many settings of public health relevance.

PubMed Disclaimer

Figures

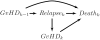
Figure 1
Figure 1
Directed acyclic graph showing hypothesized causal relationships among study variables for days k − 1 and k. This graph demonstrates bias in regression stratification methods in estimating the effect of exposure over time (GνHDk−1, GνHDk) on subsequent death when time-varying factors on confounding pathways (Relapsek) may be affected by prior exposure.
Figure 2
Figure 2
Parametric g-formula algorithm for bone marrow transplant data.
Figure 3
Figure 3
Incidence curves for (A.) death. (B.) return to normal platelet levels, (C.) relapse and (D.) graft-versus-host-disease (GvHD) from both observed (gray line) and g-formula natural course Monte Carlo (black line) data.
Figure 3
Figure 3
Incidence curves for (A.) death. (B.) return to normal platelet levels, (C.) relapse and (D.) graft-versus-host-disease (GvHD) from both observed (gray line) and g-formula natural course Monte Carlo (black line) data.
Figure 3
Figure 3
Incidence curves for (A.) death. (B.) return to normal platelet levels, (C.) relapse and (D.) graft-versus-host-disease (GvHD) from both observed (gray line) and g-formula natural course Monte Carlo (black line) data.
Figure 3
Figure 3
Incidence curves for (A.) death. (B.) return to normal platelet levels, (C.) relapse and (D.) graft-versus-host-disease (GvHD) from both observed (gray line) and g-formula natural course Monte Carlo (black line) data.
Figure 4
Figure 4
Survival functions: observed from the bone marrow transplant data; from the natural-course intervention in the g-formula; and from the hypothetical intervention “prevented” graft-versus-host disease (top line) after bone marrow transplants using the g-formula. The gray line indicates the observed survival curve, while the solid black lines indicate the survival curves from the Monte Carlo data for the g-formula interventions.
See this image and copyright information in PMC

Comment in

References

    1. Sullivan K, Weiden P, Storb R, Witherspoon R, Fefer A, Fisher L, Buckner C, Anasetti C, Appelbaum F, Badger C. Influence of acute and chronic graft-versus-host disease on relapse and survival after bone marrow transplantation from HLA-identical siblings as treatment of acute and chronic leukemia. Blood. 1989;73:1720–1728. published erratum appears in Blood 1989 Aug 15; 74 (3): 1180. - PubMed
    1. Horowitz MM, Gale RP, Sondel PM, Goldman JM, Kersey J, Kolb HJ, Rimm AA, Ringdén O, Rozman C, Speck B. Graft-versus-leukemia reactions after bone marrow transplantation. Blood. 1990;75:555–562. - PubMed
    1. Robins JM, Wasserman L. Estimation of effects of sequential treatments by reparameterizing directed acyclic graphs. Proceedings of the Thirteenth Conference on Uncertainty in Artificial Intelligence; 1997. pp. 409–420.
    1. Keiding N, Filiberti M, Esbjerg S, Robins JM, Jacobsen N. The graft versus leukemia effect after bone marrow transplantation: A case study using structural nested failure time models. Biometrics. 1999;55:23–28. - PubMed
    1. Hernán MA, Robins JM. Causal Inference. Boca Raton, FL: Chapman & Hall/CRC; 2013.

Publication types