Formation, habitability, and detection of extrasolar moons

Abstract

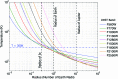
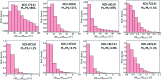
The diversity and quantity of moons in the Solar System suggest a manifold population of natural satellites exist around extrasolar planets. Of peculiar interest from an astrobiological perspective, the number of sizable moons in the stellar habitable zones may outnumber planets in these circumstellar regions. With technological and theoretical methods now allowing for the detection of sub-Earth-sized extrasolar planets, the first detection of an extrasolar moon appears feasible. In this review, we summarize formation channels of massive exomoons that are potentially detectable with current or near-future instruments. We discuss the orbital effects that govern exomoon evolution, we present a framework to characterize an exomoon's stellar plus planetary illumination as well as its tidal heating, and we address the techniques that have been proposed to search for exomoons. Most notably, we show that natural satellites in the range of 0.1-0.5 Earth mass (i) are potentially habitable, (ii) can form within the circumplanetary debris and gas disk or via capture from a binary, and (iii) are detectable with current technology.

FIG. 1.

Europa, Enceladus, Ganymede, and Titan are regarded as potentially habitable moons. Global lineaments on Europa's surface and ridges on Enceladus indicate liquid water as close as a few kilometers below their frozen surfaces. Ganymede's surface is much older, with two predominant terrains: bright, grooved areas and older, heavily cratered, dark regions. Titan has a dense nitrogen atmosphere and liquid methane/ethane seas on its surface. While the atmosphere is intransparent to the human eye, the lower right image contains information taken in the infrared. Note the different scales! Moon diameters are indicated below each satellite. (Image credits: NASA/JPL/Space Science Institute/Ted Stryk) (Color images available online at www.liebertonline.com/ast)

FIG. 2.

Results after 100 simulations of moon formation around a 10 M_Jup planet. Left panel: Multiplicity distribution of the produced satellite systems for satellite masses M_s>10⁻² M_⊕. Right panel: Averaged M_s and semimajor axis (a) are shown as filled circles; their standard deviations are indicated by error bars for the 36 four-satellite systems.

FIG. 3.

Maximum captured mass (ordinate) as a function of escaping mass (abscissa) and encounter distance b=5 R_p, 10 R_p, and 15 R_p (contours). The curves are calculated from Eq. 3 with the planetary mass set to 0.3 M_Jup and the distance from the K star a_★=0.8 AU in both panels. The encounter speed at infinity is v_∞=0.5 km/s in the left panel and v_∞=5 km/s in the right panel.

FIG. 4.

Tidal evolution of an Earth-sized moon orbiting a Jupiter-sized planet. Left panels: Semimajor axis (top) and obliquity (bottom) evolution for different initial semimajor axes, while all other initial parameters are equal. The black dashed-dotted line in the top panel represents the planetary radius; four overlapping dashed lines indicate the corotation radii. A red dashed line represents the Roche limit. Right panels: Semimajor axis (top) and eccentricity (bottom) evolution for the same system but for different initial eccentricities. (Color graphics available online at www.liebertonline.com/ast)

FIG. 5.

Evolution of the semimajor axes (a_ps) and eccentricities (e_ps) of the two satellites orbiting a Jupiter-mass planet. Red lines correspond to the inner Mars-mass satellite, blue lines to the outer Earth-mass satellite, and black lines represent the corotation distance. Each panel depicts a different initial distance for the outer satellite, increasing from panels 1 to 9. (Color graphics available online at www.liebertonline.com/ast)

FIG. 6.

Evolution of the obliquity (top left), inclination (center left), rotation period (bottom left), and internal heat flux (right) of a Mars-like (red lines) and an Earth-like (blue lines) satellite orbiting a Jupiter-mass planet (configuration of panel 2 in Fig. 5). In the bottom left panel, the black line represents the rotation period of the planet, and the dashed lines correspond to the pseudo-synchronization period of the satellites. In the right panel, the dotted black horizontal line corresponds to the internal heat flux of Earth (0.08 W/m²); the dashed black lines correspond to tidal surface heating on Io (2.4–4.8 W/m²). (Color graphics available online at www.liebertonline.com/ast)

FIG. 7.

Circumplanetary HEs for a Mars-mass (orange lines) and an Earth-mass (blue lines) exomoon orbiting a range of host planets (masses indicated along the ordinate). All systems are assumed to be at 1 AU from a Sun-like star. HEs are indicated for four different orbital eccentricities: . The larger the e_ps, the farther away the moons need to be around a given planet to avoid transition into a runaway greenhouse due to extensive tidal heating. Examples for the orbital distances found in the jovian and saturnian satellite systems are indicated with labeled dots. (Color graphics available online at www.liebertonline.com/ast)

FIG. 8.

Circumplanetary exomoon menageries for Mars-sized satellites around a 10 M_Jup host planet at ages of 100 Myr (left panel) and 1 Gyr (right panel). The planet is assumed to orbit in the middle of the HZ of a 0.7 M_⊙ star, and the moon orbits the planet with an eccentricity of 10⁻³. In each panel, the planet's position is at (0, 0), and distances are shown on logarithmic scales. Note that exomoons in a Tidal Venus or a Tidal-Illumination Venus state are in a runaway greenhouse state and thereby uninhabitable. (Color graphics available online at www.liebertonline.com/ast)

FIG. 9.

Schematic representation of a planetary magnetosphere. Its roughly spherical dayside region has a standoff radius R_S to the planetary center. Between the bow shock and the magnetopause lies the magnetosheath, a region of shocked stellar-wind plasma and piled-up interplanetary magnetic fields. Inside the magnetosphere, plasma is dragged by the corotating magnetic field, thereby creating a particle stream called the “corotating magnetoplasma.” Moons at orbital distances<R_S (completely shielded, CS) can be subject to this magnetospheric wind and, hence, experience similar effects as unshielded (US) moons exposed to stellar wind. Partially shielded (PS) moons that spend most of their orbital path inside the magnetosphere will experience both effects of interplanetary magnetic fields and stellar wind periodically. (Color graphics available online at www.liebertonline.com/ast)

FIG. 10.

Evolution of the standoff radius R_S (thick blue line) around a Jupiter-like planet in the center of the stellar HZ of a Sun-like star. For comparison, the orbits of the Galilean moons are shown (see legend). Angles with respect to the vertical line encode time in billions of years. Time starts at the “12:00” position in 100 Myr and advances in steps of 0.3 Gyr up to the present age of the Solar System. Thin gray circles denote distances in intervals of 5 planetary radii. The filled circle in the center denotes the planetary radius. (Color graphics available online at www.liebertonline.com/ast)

FIG. 11.

Period-ratio versus mass-ratio scatter plot of the Solar System moons. Transit timing and duration variations (TTV and TDV) exhibit complementary sensitivities with the period-ratio. Using the Kepler timing measurements from Ford et al. (2012), one can see that the tip of the observed distribution is detectable. The above assumes a planetary period of 100 days and a baseline of 4.35 yr of Kepler data. (Color graphics available online at www.liebertonline.com/ast)

FIG. 12.

(Left) Six simulated transits using LUNA (Kipping, 2011b) of a HZ Neptune around an M2 star with an Earth-like moon on a wide orbit (90% of the Hill radius). The moon can be seen to exhibit “auxiliary transits” and induce TTV. (Right) Same as left, except the moon is now on a close-in orbit (5% of the Hill radius), causing “mutual events.” Both plots show typical Kepler noise properties for a 12^th-magnitude star observed in short cadence.

FIG. 13.

Transit of the almost Jupiter-sized planet candidate KOI189.01 around a star of about 0.7 solar radii. Gray dots indicate the original phase-folded Kepler light curve, the black dashed line indicates a model for the transit assuming a planet only, and the red line assumes an Earth-sized moon in an orbit that is 15 planetary radii wide. Black dots in the right panel indicate data that is binned to 60 min. The photometric orbital sampling effect appears in the right panel as a deviation between the red solid and the black dashed line about 6.5 h before the planetary midtransit. (Color graphics available online at www.liebertonline.com/ast)

FIG. 14.

Calculated timing errors of the transit mid-time (filled circles) and duration (open circles) for Kepler planet candidates around stars with magnitudes<13.5 (Mazeh et al., 2013). Planetary radii are estimated by assuming an Earth-like composition (left panel) or a mostly gaseous composition (right panel). Point size is proportional to the stellar radius, with color indicating if the radius is smaller than 0.7 solar radii (R_⊙) (red), between 0.7 and 1.3 R_⊙ (gold), or larger than 1.3 R_⊙ (green). Predictions of the errors in transit mid-time (solid line) and duration (dotted line) following Carter et al. (2008) assume a central transit and white noise for the case of a 1 or 10 R_⊕ radius planet orbiting a 0.7 R_⊙ (red), R_⊙ (gold), or 1.3 R_⊙ (green) star. Photometric transit timing errors, dominated by white noise (dashed line) and realistic solar-type noise (crosses) assume a 12^th-magnitude G dwarf and relative photometric precision of 2×10⁻⁵ in a 6.5 h exposure (Lewis, 2013). (Color graphics available online at www.liebertonline.com/ast)

FIG. 15.

5σ detection limits of JWST's MIRI for THEMs with radii along the abscissa and effective temperatures along the ordinate (following Turner and Peters, 2013). Ten thousand seconds of integration are assumed for a star 3 pc from the Sun. MIRI's nine imaging bands are indicated with different line colors, their names encoding the wavelength in units of microns times 100. Dashed vertical black lines denote the radii of Io, Earth, and Jupiter, which is roughly equal to that of a typical brown dwarf. (Color graphics available online at www.liebertonline.com/ast)

FIG. 16.

Minimum detectable eccentricity (abscissa) and semimajor axis in units of Roche radii (β_ps, ordinate) for THEMs between 0.1 and 1 R_⊕ in size (Turner and Peters, 2013). The assumed bodily characteristics are described around Eqs. 5–6. The orange dot indicates Io's eccentricity and β_ps, but note that its size is 0.066 R_⊕. Satellites below their respective curve will be detectable by MIRI as far as 3 pc from Earth, provided they are sufficiently separated from their star. (Color graphics available online at www.liebertonline.com/ast)

FIG. 17.

Moon-to-planet mass ratio constraints derived so far by the HEK project (Nesvorný et al., ; Kipping et al., 2013a). Kepler-22b has also been studied and yields M_s<0.5 M_⊕ but is not shown here, as the paper is still under review at the time of writing. (Color graphics available online at www.liebertonline.com/ast)