Simulated cytoskeletal collapse via tau degradation
- PMID: 25162587
- PMCID: PMC4146510
- DOI: 10.1371/journal.pone.0104965
Simulated cytoskeletal collapse via tau degradation
Abstract
We present a coarse-grained two dimensional mechanical model for the microtubule-tau bundles in neuronal axons in which we remove taus, as can happen in various neurodegenerative conditions such as Alzheimers disease, tauopathies, and chronic traumatic encephalopathy. Our simplified model includes (i) taus modeled as entropic springs between microtubules, (ii) removal of taus from the bundles due to phosphorylation, and (iii) a possible depletion force between microtubules due to these dissociated phosphorylated taus. We equilibrate upon tau removal using steepest descent relaxation. In the absence of the depletion force, the transverse rigidity to radial compression of the bundles falls to zero at about 60% tau occupancy, in agreement with standard percolation theory results. However, with the attractive depletion force, spring removal leads to a first order collapse of the bundles over a wide range of tau occupancies for physiologically realizable conditions. While our simplest calculations assume a constant concentration of microtubule intercalants to mediate the depletion force, including a dependence that is linear in the detached taus yields the same collapse. Applying percolation theory to removal of taus at microtubule tips, which are likely to be the protective sites against dynamic instability, we argue that the microtubule instability can only obtain at low tau occupancy, from 0.06-0.30 depending upon the tau coordination at the microtubule tips. Hence, the collapse we discover is likely to be more robust over a wide range of tau occupancies than the dynamic instability. We suggest in vitro tests of our predicted collapse.
Conflict of interest statement
Figures
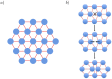
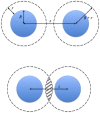
 is depleted of intercalants. The loss of excluded volume as the microtubules approach allows increased translational entropy outside the bundle for the intercalants.
is depleted of intercalants. The loss of excluded volume as the microtubules approach allows increased translational entropy outside the bundle for the intercalants.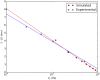
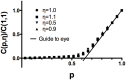
 and (b) scale to the
and (b) scale to the  limit. In contrast to Ref. , all
limit. In contrast to Ref. , all  values yield the same results when scaled, because their lattice boundary is fixed while ours relax to equilibrium. In all cases, the transverse rigidity percolation threshold is
values yield the same results when scaled, because their lattice boundary is fixed while ours relax to equilibrium. In all cases, the transverse rigidity percolation threshold is  , in good agreement with the
, in good agreement with the  case of Ref.
case of Ref.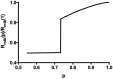
 is reduced from 1, for the dimensionless parameter
is reduced from 1, for the dimensionless parameter  After a gradual reduction of
After a gradual reduction of  for
for  , the depletion force overwhelms the entropic springs at
, the depletion force overwhelms the entropic springs at  = 0.73.
= 0.73.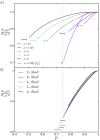
 with the leftmost end at
with the leftmost end at  . a) The MTBs undergo a first order collapse with reduced
. a) The MTBs undergo a first order collapse with reduced  , with the collapse onset decreasing with
, with the collapse onset decreasing with  for fixed spring constant
for fixed spring constant  = 0.05 pN/nm. The lavender curve is computed with the same
= 0.05 pN/nm. The lavender curve is computed with the same  value at collapse as the blue curve but for an osmotic pressure proportional to
value at collapse as the blue curve but for an osmotic pressure proportional to  . For
. For  (not shown) the radius
(not shown) the radius  is that of hexagaonally close packed microtubules. b) For varying initial bundle radius, measured by the number of hexagonal shells retained about the central MT, the normalized radius displays the collapse at the same location for a fixed value of
is that of hexagaonally close packed microtubules. b) For varying initial bundle radius, measured by the number of hexagonal shells retained about the central MT, the normalized radius displays the collapse at the same location for a fixed value of  = 3.125, indicating the collapse is not an artifact of finite size.
= 3.125, indicating the collapse is not an artifact of finite size.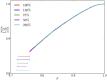
 with the leftmost end at
with the leftmost end at  . Here we carry out the simulations multiplying
. Here we carry out the simulations multiplying  independently by the percentages shown in the legend to achieve the same
independently by the percentages shown in the legend to achieve the same  value. Clearly this gives the same
value. Clearly this gives the same  for collapse onset.
for collapse onset.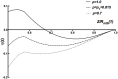
 vs. scaled mean microtubule separation
vs. scaled mean microtubule separation  for
for  nm and
nm and  = 3.125. As
= 3.125. As  is reduced, the potential at
is reduced, the potential at  which is the separation at microtubule contact, reaches a lower value than the minimum which evolves from
which is the separation at microtubule contact, reaches a lower value than the minimum which evolves from  at
at  .
.
 vs.
vs.  for the MFT and the full simulations. Clearly, the MFT and full simulation trends are very similar.
for the MFT and the full simulations. Clearly, the MFT and full simulation trends are very similar.References
-
- Hardy JA, Higgins GA (1992) The amyloid cascade hypothesis. Science 256: 184–185. - PubMed
-
- Hardy JA, Selkoe DJ (2002) The amyloid hypothesis of alzheimer's disease: progress and problems on the road to therapeutics. Science 297: 353–356. - PubMed
-
- Wang JZ, Liu F (2008) Microtubule-associated protein tau in development, degeneration, and protection of neurons. Progress in Neurobiology 85: 148–175. - PubMed
Publication types
MeSH terms
Substances
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources

