Collective foraging in heterogeneous landscapes
- PMID: 25165596
- PMCID: PMC4191093
- DOI: 10.1098/rsif.2014.0674
Collective foraging in heterogeneous landscapes
Abstract
Animals foraging alone are hypothesized to optimize the encounter rates with resources through Lévy walks. However, the issue of how the interactions between multiple foragers influence their search efficiency is still not completely understood. To address this, we consider a model to study the optimal strategy for a group of foragers searching for targets distributed heterogeneously. In our model, foragers move on a square lattice containing immobile but regenerative targets. At any instant, a forager is able to detect only those targets that happen to be in the same site. However, we allow the foragers to have information about the state of other foragers. A forager who has not detected any target walks towards the nearest location, where another forager has detected a target, with a probability exp(-αd), where d is the distance between the foragers and α is a parameter characterizing the propensity of the foragers to aggregate. The model reveals that neither overcrowding (α → 0) nor independent searching (α → ∞) is beneficial for the foragers. For a patchy distribution of targets, the efficiency is maximum for intermediate values of α. In addition, in the limit α → 0, the length of the walks can become scale-free.
Keywords: Lévy walks; heterogeneous landscapes; optimal foraging theory.
© 2014 The Author(s) Published by the Royal Society. All rights reserved.
Figures


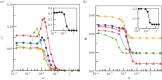


 gives the value of μ = 2.80. In (c), the values of μ corresponding to different values of N (=L) resulting from regression fits are provided in the legend. (Online version in colour.)
gives the value of μ = 2.80. In (c), the values of μ corresponding to different values of N (=L) resulting from regression fits are provided in the legend. (Online version in colour.)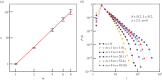
 . The bars indicate the standard deviations obtained from averaging over time snapshots and initial conditions. The straight line corresponds to a power-law fit having exponent equal to 2.23. (b) The plots of probability density function, P(l), of the length of targeted walks when α = 0, corresponding to different values of m as indicated in the legend. (Online version in colour.)
. The bars indicate the standard deviations obtained from averaging over time snapshots and initial conditions. The straight line corresponds to a power-law fit having exponent equal to 2.23. (b) The plots of probability density function, P(l), of the length of targeted walks when α = 0, corresponding to different values of m as indicated in the legend. (Online version in colour.)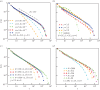
 give the value of δ = 1.67 for all three values of α. In (c), the values of δ corresponding to different values of N (=L) resulting from regression fits are provided in the legend. (Online version in colour.)
give the value of δ = 1.67 for all three values of α. In (c), the values of δ corresponding to different values of N (=L) resulting from regression fits are provided in the legend. (Online version in colour.)References
-
- Bartumeus F, Catalan J. 2009. Optimal search behavior and classic foraging theory. J. Phys. A: Math. Theor. 42, 434002 (10.1088/1751-8113/42/43/434002) - DOI
-
- Pitcher TJ, Magurran AE, Winfield IJ. 1982. Fish in larger shoals find food faster. Behav. Ecol. Sociobiol. 10, 149–151. (10.1007/BF00300175) - DOI
-
- Haney JC, Fristrup KM, Lee DS. 1992. Geometry of visual recruitment by seabirds to ephemeral foraging flocks. Ornis Scand. 23, 49–62. (10.2307/3676427) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

