Classical mathematical models for description and prediction of experimental tumor growth

Abstract

Despite internal complexity, tumor growth kinetics follow relatively simple laws that can be expressed as mathematical models. To explore this further, quantitative analysis of the most classical of these were performed. The models were assessed against data from two in vivo experimental systems: an ectopic syngeneic tumor (Lewis lung carcinoma) and an orthotopically xenografted human breast carcinoma. The goals were threefold: 1) to determine a statistical model for description of the measurement error, 2) to establish the descriptive power of each model, using several goodness-of-fit metrics and a study of parametric identifiability, and 3) to assess the models' ability to forecast future tumor growth. The models included in the study comprised the exponential, exponential-linear, power law, Gompertz, logistic, generalized logistic, von Bertalanffy and a model with dynamic carrying capacity. For the breast data, the dynamics were best captured by the Gompertz and exponential-linear models. The latter also exhibited the highest predictive power, with excellent prediction scores (≥80%) extending out as far as 12 days in the future. For the lung data, the Gompertz and power law models provided the most parsimonious and parametrically identifiable description. However, not one of the models was able to achieve a substantial prediction rate (≥70%) beyond the next day data point. In this context, adjunction of a priori information on the parameter distribution led to considerable improvement. For instance, forecast success rates went from 14.9% to 62.7% when using the power law model to predict the full future tumor growth curves, using just three data points. These results not only have important implications for biological theories of tumor growth and the use of mathematical modeling in preclinical anti-cancer drug investigations, but also may assist in defining how mathematical models could serve as potential prognostic tools in the clinic.

Figure 1. Volume measurement error.

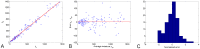
A. First measured volume y ₁ against second one y ₂. Also plotted is the regression line (correlation coefficient R = 0.98, slope of the regression  = 0.96). B. Error against approximation of the volume given by the average of the two measurement . The χ ² test rejected Gaussian distribution of constant variance () C. Histogram of the normalized error applying the error model given by with α = 0.84 and V_m = 83 mm³. It shows Gaussian distribution (χ ² test not rejected, p = 0.196) with standard deviation .

Figure 2. Descriptive power of the models for lung and breast tumor data.

A. Representative examples of all growth models fitting the same growth curve (animal 10 for lung, animal 14 for breast). Error bars correspond to the standard deviation of the a priori estimate of measurement error. In the lung setting, curves of the Gompertz, power law, dynamic CC and von Bertalanffy models are visually indistinguishable. B. Corresponding relative growth rate curves. Curves for von Bertalanffy and power law are identical in the lung setting. C. Residuals distributions, in ascending order of mean RMSE (13) over all animals. Residuals (see formula (15) for their definition) include fits over all the animals and all the time points. Exp1 = exponential 1, Exp-L = exponential-linear, Exp V ₀ = exponential V ₀, Log = logistic, GLog = generalized logistic, PL = power law, Gomp = Gompertz, VonBert = von Bertalanffy, DynCC = dynamic CC.

Figure 3. Examples of predictive power.

Representative examples of the forecast performances of the models for the lung data set (mouse number 2). Five data points were used to estimate the animal parameters and predict future growth. Prediction success of the models are reported for the next day data point (OK₁) or global future curve (OK_glob), based on the criterion of a normalized error smaller than 3 (meaning that the model prediction is within 3 standard deviations of the measurement error) for OK₁ and the median of this metric over the future curve for OK_glob (see Materials and Methods for details).

Figure 4. Prediction depth and number of data points.

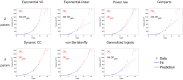
Predictive power of some representative models depending on the number of data points used for estimation of the parameters (n) and the prediction depth in the future (d). Top: at position (n,d) the color represents the percentage of successfully predicted animals when using n data points and forecasting the time point , as quantified by the score (multiplied by 100), defined in (17). This proportion only includes animals having measurements at these two time points, thus values at different row d on the same column n or reverse might represent predictions in different animals. White squares correspond to situations where this number was too low (<5) and thus success score, considered not significant, was not reported. Bottom: distribution of the relative error of prediction (20), all animals and (n,d) pooled together. Models were ranked in ascending order of overall mean success score reported in Tables 5 and 6. A. Lung tumor data. B. Breast tumor data.

Figure 5. A priori information and improvement of prediction success rates.

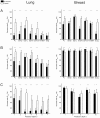
Predictions were considered when randomly dividing the animals between two equal groups, one used for learning the parameters distribution and the other for prediction, using n = 3 data points. Success rates are reported as mean ± standard deviation over 100 random partitions into two groups. A. Prediction of global future curve, quantified by the score (see Materials and Methods, Models predictions methods for its definition). B. Benefit of the method for prediction of the next day, using three data points (score ). C. Prediction improvement at various prediction depths, using the power law model (lung data) or the exponential-linear model (breast data). Due to lack of animals to be predicted for some of the random assignments, results of depths 2, 4, 6 and 9 for the breast data were not considered significant and were not reported (see Materials and Methods). * = p<0.05, ** = p<0.001, Student's t-test.