k-t FASTER: Acceleration of functional MRI data acquisition using low rank constraints

Abstract

Purpose: In functional MRI (fMRI), faster sampling of data can provide richer temporal information and increase temporal degrees of freedom. However, acceleration is generally performed on a volume-by-volume basis, without consideration of the intrinsic spatio-temporal data structure. We present a novel method for accelerating fMRI data acquisition, k-t FASTER (FMRI Accelerated in Space-time via Truncation of Effective Rank), which exploits the low-rank structure of fMRI data.

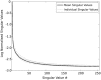
Theory and methods: Using matrix completion, 4.27× retrospectively and prospectively under-sampled data were reconstructed (coil-independently) using an iterative nonlinear algorithm, and compared with several different reconstruction strategies. Matrix reconstruction error was evaluated; a dual regression analysis was performed to determine fidelity of recovered fMRI resting state networks (RSNs).

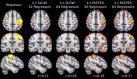
Results: The retrospective sampling data showed that k-t FASTER produced the lowest error, approximately 3-4%, and the highest quality RSNs. These results were validated in prospectively under-sampled experiments, with k-t FASTER producing better identification of RSNs than fully sampled acquisitions of the same duration.

Conclusion: With k-t FASTER, incoherently under-sampled fMRI data can be robustly recovered using only rank constraints. This technique can be used to improve the speed of fMRI sampling, particularly for multivariate analyses such as temporal independent component analysis.

Keywords: compressed sensing; fMRI; k-t acceleration; low-rank acceleration; matrix completion; resting state networks.

Figure 1

Schematic diagram illustrating the motivation for the k-t FASTER acceleration strategy. In the standard imaging approach, the full k-t matrix is acquired using conventional fMRI acquisition methods. As a preprocessing step, dimensionality reduction is performed by means of PCA, and information is discarded. Using k-t FASTER, the k-t matrix is under-sampled, and a matrix completion algorithm is used to directly reconstruct a rank-constrained dataset.

Figure 2

Normalized singular values from fMRI data with 512 time points. These singular value decays reflect approximately low rank nature of fMRI data, where after mean centering, > 80% of the signal variance is captured in the top 25% components. Dashed lines represent fMRI data from six different subjects, with mean values indicated with the solid line.

Figure 3

Representative diagrams of the different k_z-t under-sampling patterns studied. Pseudorandom under-sampling (a), sheared grid under-sampling (b), and temporal under-sampling (i.e., standard low-temporal resolution) (c). In all cases, in-plane (k_x-k_y) data are fully sampled.

Figure 4

a: Example portion of a magnitude k-space time-series from a k-t FASTER reconstruction (red), compared with the ground truth (grey) and a rank-128 ground truth time-series (blue). The k-t FASTER data reproduce many dynamic features of the ground truth in between sampled points. Arrows point to features that are common to the k-t FASTER and rank-128 time-series, suggesting that they reflect the rank constraints rather than errors intrinsic to the k-t FASTER method. b: Example voxel time-series segment similarly showing good recovery of dynamic features in the k-t FASTER reconstruction.

Figure 5

a: Relative Frobenius norm errors for all six subjects, across the three different reconstruction methods and the rank-128 dimensionality reduction of the ground truth data. b: Frobenius norm errors normalized to the error in the rank-128 truth data, highlighting the excellent performance of the k-t FASTER method compared with the k-t PSF and k-t INTERP methods.

Figure 6

a: Mean z-statistic map correlations for the reconstructed data compared to the canonical input regressors. b: Direct correlation of the z-statistic maps for each method with the truth maps, which show that the k-t FASTER maps match the truth maps best. In both cases, error bars denote standard deviation.

Figure 7

Z-stat image dual regression output for a single dataset for a regressor corresponding to an occipital (visual) resting state network. All images are un-thresholded with color scale mapped between 0 < |z| < 6.

Figure 8

Z-stat image dual regression output for a single dataset for a regressor corresponding bilateral parietal resting state network. All images are un-thresholded with color scale mapped between 0 < |z| < 4.

Figure 9

Boxplot of correlation coefficients from the dual regression averaged across scans and 32 maps for each of the six subjects, using both 32 and 64 regressors.

Figure 10

Z-stat image dual regression output for a single subject for a regressor corresponding to left somatosensory resting state network. Correlation coefficients with the canonical regressors are shown at the bottom of the images. All maps are thresholded at |z|>2 and with color scale mapped between 2 < |z| < 6, except for the regressor maps, which are scaled and thresholded at 10×.