Fast convergence of learning requires plasticity between inferior olive and deep cerebellar nuclei in a manipulation task: a closed-loop robotic simulation

Abstract

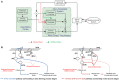
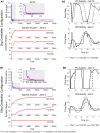
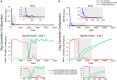
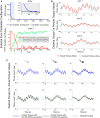
The cerebellum is known to play a critical role in learning relevant patterns of activity for adaptive motor control, but the underlying network mechanisms are only partly understood. The classical long-term synaptic plasticity between parallel fibers (PFs) and Purkinje cells (PCs), which is driven by the inferior olive (IO), can only account for limited aspects of learning. Recently, the role of additional forms of plasticity in the granular layer, molecular layer and deep cerebellar nuclei (DCN) has been considered. In particular, learning at DCN synapses allows for generalization, but convergence to a stable state requires hundreds of repetitions. In this paper we have explored the putative role of the IO-DCN connection by endowing it with adaptable weights and exploring its implications in a closed-loop robotic manipulation task. Our results show that IO-DCN plasticity accelerates convergence of learning by up to two orders of magnitude without conflicting with the generalization properties conferred by DCN plasticity. Thus, this model suggests that multiple distributed learning mechanisms provide a key for explaining the complex properties of procedural learning and open up new experimental questions for synaptic plasticity in the cerebellar network.

Keywords: cerebellar nuclei; inferior olive; learning consolidation; long-term synaptic plasticity; modeling.

Figure 1

The cerebellum operating in a feedforward control system. (A) The mossy fibers are thought to provide information referring to the desired plant motor output from motor cortex and the current sensory information referring to the actual state of the body parts (i.e., joint positions/velocities of the upper-limbs of the body-plant). According to the Marr–Albus model (Marr, ; Albus, 1971) the climbing fibers are assumed to carry error-related information when moving, thus providing a teaching signal to the cerebellum. By using this error-based-teaching signal the cerebellum is able to learn the corrective actions in a trial-and-error process. When the cerebellar model is not able to deliver add-on torque terms to compensate deviations in the system (for instance during the early learning stages) the general rule consists of adding a feedback to stabilize the open-loop system. (B) Different control pathways during the learning process. The relevant information flow is represented by dashed lines in each learning stage. A fast response gain control is delivered by IO-DCN connection, thus supplying stability in early learning-process stages (dashed blue lines). In later learning-process stages the two control pathways (dashed red lines); the internal MF-GrC-PC-DCN and the more external MF-DCN command the control action. Whilst IO-DCN action decays throughout the learning process its control action is assumed and improved by these two long-term adaptive pathways.

Figure 2

Cerebellar control loop and benchmark trajectory. (A) The adaptive cerebellar module delivers corrective torque values (τ_corrective) to compensate for deviations in the crude inverse dynamic module when manipulating an object of significant weight. In this feedforward control loop, the cerebellum receives a teaching error-dependent signal and the desired arm state (Q_d, ${\dot{Q}}_d$, ${\ddot{Q}}_d$) so as to produce the adaptive corrective actions. (B) Three-joint periodic benchmark trajectory suitable for testing the kinematic and dynamical properties of the robot arm and the application area. Fast movements in a smooth pursuit task composed of vertical and horizontal sinusoidal components are able to reveal the whole robot arm dynamic properties (Hoffmann and Petkos, 2007). The left panel represents angular coordinate per joint followed by the light weight robot, the right panel plots the robot end-effector trajectory in euclidean space.

Figure 3

Learning generalization by means of distributed plasticity. The system gain (external to the cerebellum) was properly set to manipulate accurately the robot-arm without any object (no external payload). Since the manipulated mass (payload) was not expected, the existing plasticity mechanisms at MF-DCN and PC-DCN had to adjust the cerebellar output to cope with this mass (2 kg/10 kg mass configuration). (A1) Performance and learning when manipulating 2 kg mass. Evolution of the average MAE of the three robot joints during the learning process, 5000 trials. In the initial learning trials (zoom in) the MAE averaged value was about 10 times greater than the obtained MAE average value at the end of the learning process. MF-DCN and PC-DCN adjustments took about 500 iterations to be set, meanwhile the cerebellar system was working in open-loop and no action control was appropriately delivered. Plasticity occurred at PF-PC, MF-DCN, and PC-DCN synapses. The evolution of synaptic weights at MF-DCN, PC-DCN connections related to join 2 agonist muscle is also shown. For the sake of clarity only the behavior of this second joint is shown, however similar results were found throughout the learning process in both joints 1 and 3. MF-DCN and PC-DCN synaptic weight stabilization was obtained from the 500th trial. (A2) Normalized PC Firing rate (top) and DCN firing rate (bottom) during different trials taken from the initial stages of the learning process: trial 1, trial 250, and trial 500. MF-DCN and PC-DCN synaptic weight adjustments allowed the PC/DCN firing rate to operate in a proper range. (B1) Performance and learning when manipulating 10 kg mass. Evolution of the average MAE of the three robot joints during the learning process, 5000 trials. In the initial learning trials (zoom in) the MAE averaged value was, roughly speaking, more than 30 times greater than the obtained MAE average value at the end of the learning process. MF-DCN and PC-DCN adjustments took about 1000 iterations to settle down, meanwhile the cerebellar system was working in open-loop, and hence no action control was appropriately delivered. Plasticity occurred at PF-PC, MF-DCN, and PC-DCN synapses. The evolution of synaptic weights at MF-DCN, PC-DCN connections related to join 2 agonist muscle is also shown. For the sake of clarity only the behavior of this second joint is shown, however similar results were found throughout the learning process in both joints 1 and 3. MF-DCN and PC-DCN synaptic weight stabilization was obtained from the 3000th trial. (B2) Normalized PC firing rate (top) and DCN firing rate (bottom) during different trials taken from the initial stages of the learning process: trial 1, trial 500, and trial 1000. MF-DCN and PC-DCN synaptic weight adjustments allowed the PC/DCN firing rate to operate in a proper range.

Figure 4

Weight evolution in the cerebellar model manipulating different payloads with IO-DCN connection operating with multiple plasticity mechanisms. Simulations were performed using plasticity mechanisms at PF-PC, MF-DCN, and PC-DCN synapses using a custom-configured IO-DCN connection for manipulating 2 and 10 kg external payloads during 5000 trials. The initial cerebellar system gain was properly set to operate with no payload. (A1,B1) Evolution of the average MAEs of the three robot joints during the learning process for 2 and 10 kg payloads respectively with/without IO-DCN fixed synaptic weights plus cerebellum or with just the IO-DCN connection. Note that the configuration without IO-DCN connection adjusted the DCN gain after approximately 500/1000 (2 kg/10 kg configuration) trials on average. From the first trial to the 500th/1000th (2 kg/10 kg configuration) the cerebellar system worked almost in open loop, no remarkable corrective action was applied by the cerebellar adapting system. The configurations with or just IO-DCN connection were capable of supplying a proper adjustment from the beginning of the learning process. (A2,B2) Evolution of synaptic weights at IO-DCN, MF-DCN, and PC-DCN connections related to join 2 agonist muscle. For the sake of clarity only the behavior of this second joint is shown, however similar results were found along the learning process in both joints 1 and 3. MF-DCN and PC-DCN weights stabilized in about 500/3000 trials (2 kg/10 kg configuration) at different convergence speeds. This slow convergence was the consequence of the existing inter-dependence between the PC-DCN learning and the DCN activity which also depended on both MF-DCN and PC-DCN adaptation. IO-DCN connection supplied cerebellar control action whilst MF-DCN and PC-DCN synaptic weights were not stable yet.

Figure 5

Normalized synaptic contribution of each DCN afferent throughout the learning process evolution using a self-adaptable IO-DCN connection. Simulations were performed using plasticity mechanisms at PF-PC, MF-DCN, and PC-DCN synapses using a self-adaptive plasticity mechanism at IO-DCN connection for manipulating 2 and 10 kg external payloads during 5000 trials. The evolution of the average MAEs of the three robot joints during the learning process for 2 kg (A) and 10 kg payloads (B) with a cerebellum equipped with IO-DCN connection with/without self-adaptive synaptic weights is presented. The initial cerebellar system gain was properly set to operate with no payload. Since the manipulated masses were unexpected, the existing plasticity mechanisms at MF-DCN and PC-DCN adjusted the cerebellar output to cope with these masses. At initial learning stages, the cerebellar model presenting an adjustable IO-DCN connection provided a more accurate corrective action to properly perform the manipulation task. The distributed adaptation of IO-DCN, MF-DCN, and PC-DCN synaptic strengths when using 2 kg (A) and 10 kg payloads (B) related to join 2 agonist muscle is also presented. For the sake of clarity only the behavior of this second joint is shown, however similar results were found throughout the learning process in both joints 1 and 3. The self-adjustable IO-DCN connection was capable of supplying a proper adjustment from almost the beginning of the learning process. The control action of this connection was relevant only in early learning stages; once the learning process settled down, the IO control action became negligible (see zoom-in of normalized synaptic weight evolution plots).

Figure 6

Modulated Term impact at self-adaptive IO-DCN connection. Simulations were performed using plasticity mechanisms at PF-PC, MF-DCN, and PC-DCN synapses using a self-adaptive plasticity mechanism at IO-DCN connection for manipulating 2 kg external payload during 5000 trials. (A) Evolution of the average MAEs of the three robot joints during the learning process for a 2 kg payload with a cerebellum equipped with a self-adaptive synaptic weight IO-DCN connection. The modulating term plasticity at IO-DCN connection (see Equation 6) was ranged from base MTP/MTD values of 0.001 to 1000 respectively. The higher the values, the faster and the stabler the system converged. At values greater than 100 the system became unstable, a sort of windup effect appeared. The IO-DCN connection control command exceeded the physical limits of the robot-arm-system (it delivered a more corrective action at each integration step than the system could handle and needed). The IO-DCN connection control momentum was incapable of immediately responding to changes in the next-integration-step incoming error. (B) Normalized MAE convergences obtained during the learning process for a 2 kg payload when the modulating term plasticity at IO-DCN connection ranged from [0.001, 100].

Figure 7

MAE and synaptic strength evolution during the learning process at IO-DCN, MF-DCN, and PC-DCN synapses when an external variable force is applied to the end effector. Simulations were performed using plasticity mechanisms at PF-PC, MF-DCN, and PC-DCN synapses accompanied with a self-adaptive plasticity mechanism at IO-DCN connection under an external variable force field during 5000 trials. (A) Illustrates the mean absolute error evolution of the three robot joints during the learning process throughout 5000 trials accompanied with a zoom-in of the first 500 trials with/without the self-adaptive plasticity mechanism at IO-DCN synapses. Plot (A) also illustrates the distributed adaptation of the normalized synaptic strength evolution at MF-DCN, PC-DCN, and IO-DCN connections (for the sake of clarity just second agonist and antagonist paired joint muscle have been represented). The contribution of the IO-DCN (red line) connection from the 1st trial was maximal; but the agonist/antagonist balance was not properly settled down. Agonist IO-DCN connection supplied a position-error-base- control action, thus facilitating the proper PF-PC firing range operation. The combined contribution of MF-DCN/PC-DCN connections (green and blue lines) became strong enough from 500th trial to keep the system under control allowing a fine-tuning of agonist/antagonist balance whilst the IO-DCN contribution was progressively self-neglected. (B) Perturbing torque values resulting from force field action compared to desired torque values needed to perform the eight-like trajectory (C) Torque value evolution during the learning process for the second joint with/without the self-adaptive plasticity mechanism at IO-DCN synapses. Three time stamps were shown: 1, 500, and 1500 trial. IO-DCN contribution was responsible for correcting the initial torque output in a rough manner (first trial). With the passage of time the fine agonist/antagonist balance at MF-DCN/PC-DCN connections allowed the arm-robot-system to compensate torque deviations due to force field action.