Biophysical implications of lipid bilayer rheometry for mechanosensitive channels

Abstract

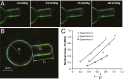
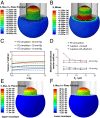
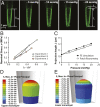
The lipid bilayer plays a crucial role in gating of mechanosensitive (MS) channels. Hence it is imperative to elucidate the rheological properties of lipid membranes. Herein we introduce a framework to characterize the mechanical properties of lipid bilayers by combining micropipette aspiration (MA) with theoretical modeling. Our results reveal that excised liposome patch fluorometry is superior to traditional cell-attached MA for measuring the intrinsic mechanical properties of lipid bilayers. The computational results also indicate that unlike the uniform bilayer tension estimated by Laplace's law, bilayer tension is not uniform across the membrane patch area. Instead, the highest tension is seen at the apex of the patch and the lowest tension is encountered near the pipette wall. More importantly, there is only a negligible difference between the stress profiles of the outer and inner monolayers in the cell-attached configuration, whereas a substantial difference (∼30%) is observed in the excised configuration. Our results have far-reaching consequences for the biophysical studies of MS channels and ion channels in general, using the patch-clamp technique, and begin to unravel the difference in activity seen between MS channels in different experimental paradigms.

Keywords: MscL; azolectin; electrophysiology; finite element modeling.

Fig. 1.

Representative cell-attached patch fluorometry experiment. (A) Confocal images of azolectin liposomal membranes fluorescently labeled by addition of 0.1% rhodamine-PE being stretched by applying four negative pressure steps of −5 to −20 mmHg. (B) L₀ is the initial projection length, and R_v and R_p denote the radius of the liposome and the micropipette, respectively. (C) Stress–strain relationship from the patch fluorometry experiment shows the variation of the nominal in-plane stress in the membrane with respect to a function of the longitudinal stretching ratio, λ − 1/λ³, for three azolectin lipid vesicles of similar diameter (6–8 µm). The relationship is fitted using the linear neo-Hookean hyperelastic model (model 3). λ is the stretching ratio in the longitudinal direction (along the length of the micropipette). These diagrams demonstrate a linear relation between the change in the nominal stress of lipid and the term λ − 1/λ³. The slope allows us to calculate the shear modulus, which is ∼1.0 MPa. R² values are 0.98, 0.94, and 0.99 for experiments 1, 2, and 3, respectively.

Fig. 2.

Spatial profiles of an aspirated liposome calculated using FE simulation. The vesicle has a diameter of 6.2 µm. The inner diameter of the micropipette is 2.8 µm (both are typical sizes encountered experimentally). The suction starts from 0 and reaches a value of −30 mmHg (∼4 kPa), instantaneously (in 0.01 s), and is then kept constant for 0.01 s. The computations are performed for the material parameters of C₁₀ = 0.5 MPa and k_b = 5.36 × 10⁻²¹ J (neo-Hookean model). (A) In-plane maximum principal stress (N/µm² distribution; maximum membrane tensional stress, σ_max, in the apex and the minimum membrane tension, 0.6 σ_max, close to the pipette wall has also been illustrated). (B) Effective stress (von Mises stress) field. (C) Comparison of membrane tension, T, at different points in the patch area using FE analysis in conjunction with the relevant Laplace’s equations for excised patch and cell-attached configurations. FE results demonstrate that there is a differential distribution of tension within a patch; with the above-mentioned geometrical properties, the cell-attached Laplace equation (solid lines) (Eq. S1) is an overestimation of the membrane tension, whereas the excised patch equation (dashed lines) (Eq. S18) underestimates the tension developed in the patch area (x axis: 0, membrane–pipette contact point; 1, patch apex). (D) Comparison of the maximum membrane tensions (in the apex) obtained from FE computation and Laplace’s law formulation at two negative pressures (blue, 10 mmHg; red, 20 mmHg) and for different vesicle sizes, R_v. This result illustrates that R_v is not affecting the actual tension distribution in the patch. However, as R_v increases, the accuracy of Eq. S1 improves up to the point where R_v = ∼9 µm. For much larger vesicles (i.e., R_v ∼ 15 µm), the results from both forms of Laplace’s equation are equal and both underestimate the actual distributed tension in the patch (Fig. S6). (E and F) Spatial profiles of the in-plane stress in an aspirated liposome illustrated in the upper (outer) monolayer and the lower (inner) monolayer, respectively. It is the same model as described in A and B, except that here, each monolayer of the bilayer has been modeled as a separate shell that can slide against another shell. Moreover, the material behavior of the inner and outer layers in the current computational model has two more material constants: their relaxation time of 0.01 and their relaxation shear modulus ratio of 0.9 (SI Materials and Methods).

Fig. 3.

Excised patch fluorometry. (A) Confocal images of a representative excised liposome patch fluorometry experiment. Rhodamine-PE–labeled azolectin liposome excised patch membranes were stretched by applying four negative pressure steps of −5 mmHg to −20 mmHg through the micropipette. L₀ is the initial projection length, L is the deformed projection length of the liposome membrane, and h is the height of the patch dome. (B) Variation of the nominal in-plane stress in the membrane with respect to the unidirectional strain term λ − 1/λ³ based on the neo-Hookean hyperelastic model. λ is the unidirectional stretching ratio in the longitudinal direction. These diagrams demonstrate a linear relation between the change in the nominal stress of lipid and the strain term λ − 1/λ³. (C) Validation of the simulations with the observations from patch fluorometry experiments. Comparisons were made between the measured aspiration lengths of azolectin lipid inside the pipette and those simulated using the neo-Hookean hyperelastic model. The inner diameters of the micropipette are typical sizes encountered experimentally. The computations were performed for the material parameters of C₁₀ = 0.71 MPa and k_b = 5.36 × 10⁻²¹ J (SI Materials and Methods). (D and E) Spatial profiles of the in-plane stress in an excised liposome patch shown in the upper (outer) monolayer and the lower (inner) monolayer, respectively. The computations were performed for the material parameters of C₁₀ = 0.71 MPa and k_b = 5.36 × 10⁻²¹ J (SI Materials and Methods). It is the same model as model described in C, except that here, each monolayer of the bilayer has been modeled as a separate surface that can slide against another surface. Moreover, the material behavior of the inner and outer layers in the current computational model has two more material constants: their relaxation time of 0.01 and their relaxation shear modulus ratio of 0.9 (SI Materials and Methods).

Fig. 4.

MS channels in the center of the patch sense a higher tensional stress than the channels close to the pipette wall. (A) In-plane maximum principal stress (MPa) distribution in a conical pipette. FE results demonstrate that there is a differential distribution of tensional stress within a patch: maximum membrane tensional stress, σ_max, in the apex and minimum tensional stress, 0.6 σ_max, close to the pipette wall (more details about the FE computations in Figs. S7 and S8). (B) Activation of MscL under a pressure ramp. Currents were recorded at a pipette voltage of +20 mV in a recording solution containing 200 mM KCl, 40 mM MgCl₂, and 5 mM Hepes-KOH, the gating kinetics of MscL under ramp pressure applied to the patch membrane. (C) “Flare-up” activation of MscL under the application of increasing pressure steps (blue arrow). Applied pressure (mmHg) is shown in red.