Error reduction in EMG signal decomposition

Abstract

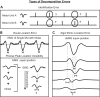
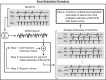
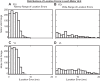
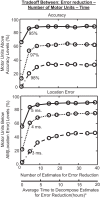
Decomposition of the electromyographic (EMG) signal into constituent action potentials and the identification of individual firing instances of each motor unit in the presence of ambient noise are inherently probabilistic processes, whether performed manually or with automated algorithms. Consequently, they are subject to errors. We set out to classify and reduce these errors by analyzing 1,061 motor-unit action-potential trains (MUAPTs), obtained by decomposing surface EMG (sEMG) signals recorded during human voluntary contractions. Decomposition errors were classified into two general categories: location errors representing variability in the temporal localization of each motor-unit firing instance and identification errors consisting of falsely detected or missed firing instances. To mitigate these errors, we developed an error-reduction algorithm that combines multiple decomposition estimates to determine a more probable estimate of motor-unit firing instances with fewer errors. The performance of the algorithm is governed by a trade-off between the yield of MUAPTs obtained above a given accuracy level and the time required to perform the decomposition. When applied to a set of sEMG signals synthesized from real MUAPTs, the identification error was reduced by an average of 1.78%, improving the accuracy to 97.0%, and the location error was reduced by an average of 1.66 ms. The error-reduction algorithm in this study is not limited to any specific decomposition strategy. Rather, we propose it be used for other decomposition methods, especially when analyzing precise motor-unit firing instances, as occurs when measuring synchronization.

Keywords: accuracy; decomposition; error reduction; motor-unit firing instances; surface EMG signal.

Fig. 1.

Pictorial representation of errors made during electromyographic (EMG) decomposition. A: when the firing instances from 2 similarly shaped motor-unit action potentials (MUAPs) occur amongst certain superpositions or noise manifestations, mistakes are likely to occur in the form of misidentifications between the firing instances of 2 motor units. These “Identification errors” consist of either falsely detected or missed firing instances and are revealed by validation of the decomposition. B: any decomposition technique is also subject to “Location errors.” During manual decomposition, superposition of noise with even a single active MUAP (MU) can blur the precise location of the action-potential peak, giving rise to location variability during template matching, measured as a location error. The location error is magnified when a manual template-matching algorithm is applied to a superposition occurrence of 2 MUAPs, a common happening during even lowest-level contractions. C: in automated decomposition, location errors occur, due to the frequent incidence of complex superpositions in the EMG signal, the resolution of which gives rise to shifts in the precise location of MUAPs, often caused by distortions of the shapes remaining within the superposition during the subtraction process. Any noise in the EMG signal would only render more difficult the determination of the precise temporal location of each firing instance. sEMG, surface EMG.

Fig. 2.

A diagrammatic depiction of the process used to generate multiple decomposition estimates for error reduction. During voluntary contraction, MUAP trains (MUAPTs), denoted MU_k, were recorded in the sEMG signal. The signal was combined with randomized Gaussian noise and subsequently decomposed to obtain an estimate of the MUAPTs, denoted dEst_i. The process of randomizing the noise, adding it to the signal, and decomposing the signal was repeated n times to obtain n slightly different estimates of the MUAPTs. These decomposition estimates were then combined to obtain a more probable estimate of the MUAPTs within the synthesized signal.

Fig. 3.

The specific decision stages used in the error-reduction algorithm. Multiple decomposition estimates, denoted dEst_i, were obtained using the procedure illustrated in Fig. 2. Three example decomposition estimates of the same MUAPT are shown. Firing instances from different decomposition estimates that represented the same motor-unit firing instance were assigned an index j. To evaluate the firing identification, each j^th firing instance was regarded as a positive identification, if and only if the firing instance was identified in ≥50% of the i^th decomposition trials, dEst_i,j. For all positive identifications of firing instances, the location of the firing instance was decided as the 1st firing instance ≥ median temporal location of all estimates of the firing instance, t_1…n,j. The final output of the error reduction provided a more probable estimate of the identification and location of each motor-unit firing instance.

Fig. 4.

Histograms of the location-error magnitude are shown in 1 ms bins for all firing instances of 1st dorsal interosseous (FDI) motor units with a (A) narrow and (B) wide range of location errors and for all firing instances of vastus lateralis (VL) motor units with a (C) narrow and (D) wide range of location errors.

Fig. 5.

The errors measured from multiple decompositions of synthesized sEMG signals are plotted as a function of the decomposition estimate number. Points plotted as “x” indicate errors measured from each of the individual, synthesized signal-decomposition estimates; points plotted as “o” indicate the errors measured from the output of error reduction, using the given number of synthesized signal-decomposition estimates. Accuracy data (1.0 − proportion of identification errors) are plotted for (A) 1 MUAPT with a relatively high initial accuracy and (B) 1 with a relatively low initial accuracy. The average magnitude of the location-error (AM{Location Error}) data is plotted for the same MUAPTs: (C) 1 with a relatively low initial AM{Location Error} and (D) another with a relatively high initial AM{Location Error}. The individual decomposition estimates manifested accuracy and AM{Location Error} values that were minimally distributed around a central mean. However, the combination of the individual estimates in the error-reduction algorithm produced new estimates with increased accuracy and decreased location-error values.

Fig. 6.

Histograms showing distributions of the (A and D) accuracy (1.0 − proportion of identification errors), (B and E) AM{Location Error}, and (C and F) mean firing rate of motor units computed from (A–C) a single decomposition estimate of the synthesized signals and (D–F) the result of error reduction using 39 synthesized signal-decomposition estimates. On average, the error-reduction algorithm improved the accuracy and reduced the location-error values, whereas mean firing rates remained largely unaffected. CI, confidence interval; pps., pulses/s.

Fig. 7.

Results illustrating the trade-off between the time required to obtain the specified number of decomposition estimates for error reduction and the number of MUAPTs obtained (top) above a given accuracy (1.0 − proportion of identification errors) threshold and (bottom) below a given AM{Location Error} threshold. The percent of 1,061 MUAPTs processed by the error-reduction algorithm is plotted for 3 different accuracy thresholds: 95% (solid line), 97% (dotted line), and 98% (dot-dash line) and 3 different AM{Location Error} thresholds: 5 ms (solid line), 4 ms (dotted line), and 3 ms (dot-dash line). The number of estimates used for error reduction to obtain the specific percentage of MUAPTs is plotted on the x-axis. Below the x-axis is another axis displaying the average time required to decompose the specified number of estimates. *The processing time is based on a Lenovo ThinkCentre computer with an Intel Core i5-2500 3.3 GHz processor and 4 gigabytes of memory, running a Windows 7 Enterprise 64-bit operating system, and averages out to ∼30 min/estimate. Generally, more MUAPTs were obtained at higher accuracy and lower AM{Location Error} levels only at the expense of a greater processing time required to decompose additional estimates for error reduction.