Stochastic optimal foraging: tuning intensive and extensive dynamics in random searches
- PMID: 25216191
- PMCID: PMC4162546
- DOI: 10.1371/journal.pone.0106373
Stochastic optimal foraging: tuning intensive and extensive dynamics in random searches
Abstract
Recent theoretical developments had laid down the proper mathematical means to understand how the structural complexity of search patterns may improve foraging efficiency. Under information-deprived scenarios and specific landscape configurations, Lévy walks and flights are known to lead to high search efficiencies. Based on a one-dimensional comparative analysis we show a mechanism by which, at random, a searcher can optimize the encounter with close and distant targets. The mechanism consists of combining an optimal diffusivity (optimally enhanced diffusion) with a minimal diffusion constant. In such a way the search dynamics adequately balances the tension between finding close and distant targets, while, at the same time, shifts the optimal balance towards relatively larger close-to-distant target encounter ratios. We find that introducing a multiscale set of reorientations ensures both a thorough local space exploration without oversampling and a fast spreading dynamics at the large scale. Lévy reorientation patterns account for these properties but other reorientation strategies providing similar statistical signatures can mimic or achieve comparable efficiencies. Hence, the present work unveils general mechanisms underlying efficient random search, beyond the Lévy model. Our results suggest that animals could tune key statistical movement properties (e.g. enhanced diffusivity, minimal diffusion constant) to cope with the very general problem of balancing out intensive and extensive random searching. We believe that theoretical developments to mechanistically understand stochastic search strategies, such as the one here proposed, are crucial to develop an empirically verifiable and comprehensive animal foraging theory.
Conflict of interest statement
Figures
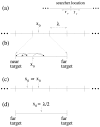
 . A detail of the searcher perceptual range (or radius of vision
. A detail of the searcher perceptual range (or radius of vision  ) is shown. (b) An example of the walk movement dynamics where a target is found after four steps. (c) In the asymmetric condition, each time the searcher finds a target, the search is re-initialized by placing it a distance
) is shown. (b) An example of the walk movement dynamics where a target is found after four steps. (c) In the asymmetric condition, each time the searcher finds a target, the search is re-initialized by placing it a distance  to the right or to the left of the target found. (d) In the symmetric starting condition,
to the right or to the left of the target found. (d) In the symmetric starting condition,  .
.
 ), (b) log-normal (
), (b) log-normal ( ), (c) stretched exponential (
), (c) stretched exponential ( ), and (d) gamma (
), and (d) gamma ( ). For all the distributions (except for the gamma), the smaller the shape parameter the heavier the tail, hence the larger the probability of large move lengths.
). For all the distributions (except for the gamma), the smaller the shape parameter the heavier the tail, hence the larger the probability of large move lengths.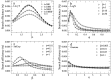
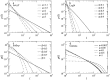
 for (a) Lévy truncated, (b) log-normal, (c) stretched exponential, and (d) gamma reorientation strategies in the asymmetric search condition. Different combinations of parameters are shown for each strategy. On the
for (a) Lévy truncated, (b) log-normal, (c) stretched exponential, and (d) gamma reorientation strategies in the asymmetric search condition. Different combinations of parameters are shown for each strategy. On the  -axes, low (large) parameter values represent ballistic (Brownian) regimes, to be compared with the heavy (non-heavy) pdf tails in Fig. 2. Maximum search efficiencies are achieved at some intermediate value of the parameters (
-axes, low (large) parameter values represent ballistic (Brownian) regimes, to be compared with the heavy (non-heavy) pdf tails in Fig. 2. Maximum search efficiencies are achieved at some intermediate value of the parameters ( -axes), except for the gamma distribution where the maximum takes place at
-axes), except for the gamma distribution where the maximum takes place at  . Notice the striking agreement between the analytical (black lines) and the numerical (symbols) results. We used parameters
. Notice the striking agreement between the analytical (black lines) and the numerical (symbols) results. We used parameters  ,
,  ,
,  , and
, and  .
.
 , analyzed to understand the relative contribution of the encounters of near (subscript
, analyzed to understand the relative contribution of the encounters of near (subscript  ) and distant (subscript
) and distant (subscript  ) targets to the global search efficiency in the asymmetric search scenario. The behavior of the traveled distances (
) targets to the global search efficiency in the asymmetric search scenario. The behavior of the traveled distances ( ,
,  , and
, and  ) and the partial quantities (
) and the partial quantities ( ,
,  ,
,  ,
,  ) is shown for each pdf model. Except for the gamma model, the search dynamics goes from ballistic to Brownian with increasing shape parameters (compare across
) is shown for each pdf model. Except for the gamma model, the search dynamics goes from ballistic to Brownian with increasing shape parameters (compare across  -axes with Fig. 2). The scale parameters are fixed at the search optimal. Note that the minimal
-axes with Fig. 2). The scale parameters are fixed at the search optimal. Note that the minimal  is close to the minimal
is close to the minimal  , suggesting that, in the asymmetric search condition, the encounter efficiency of distant targets is relevant to the global search efficiency. However, the precise optimal strategy in each case results from the subtle balance between exploring nearby areas and accessing faraway regions. Analytical (black lines) and numerical (symbols) results are displayed with nice agreement. We used parameters
, suggesting that, in the asymmetric search condition, the encounter efficiency of distant targets is relevant to the global search efficiency. However, the precise optimal strategy in each case results from the subtle balance between exploring nearby areas and accessing faraway regions. Analytical (black lines) and numerical (symbols) results are displayed with nice agreement. We used parameters  ,
,  ,
,  , and
, and  .
.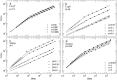
 (for some of the parametrization), coinciding with the parameter
(for some of the parametrization), coinciding with the parameter  . Solid lines: numerical simulations. Symbols: analytical results for both the short-term first-passage-time regime,
. Solid lines: numerical simulations. Symbols: analytical results for both the short-term first-passage-time regime,  , defined in Eq. (9) (open symbols), and the long-term Brownian regime, defined in Eq. (12) (filled symbols). Notice the nice agreement between numerical and analytical results. We used parameters
, defined in Eq. (9) (open symbols), and the long-term Brownian regime, defined in Eq. (12) (filled symbols). Notice the nice agreement between numerical and analytical results. We used parameters  ,
,  ,
,  , and
, and  .
.
 (a,b), and for any initial condition
(a,b), and for any initial condition  (c,d). Panels a and b: r.m.s. behavior (a) and values for the diffusion constant, diffusion exponent, and close-to-distant encounter ratio
(c,d). Panels a and b: r.m.s. behavior (a) and values for the diffusion constant, diffusion exponent, and close-to-distant encounter ratio  (b) at the asymmetric search condition (
(b) at the asymmetric search condition ( ,
,  , and
, and  ). Parameter values as follows: Lévy truncated (
). Parameter values as follows: Lévy truncated ( ,
,  ), log-normal (
), log-normal ( ,
,  ), stretched exponential (
), stretched exponential ( ,
,  ) and gamma (
) and gamma ( ,
,  ). Solid brown lines show the r.m.s. behavior (a) and the diffusion exponent (b) for a non-truncated Lévy reorientation strategy with Lévy index
). Solid brown lines show the r.m.s. behavior (a) and the diffusion exponent (b) for a non-truncated Lévy reorientation strategy with Lévy index  . Panels c and d: search efficiency (c) and
. Panels c and d: search efficiency (c) and  -ratio (d) for the optimal reorientation strategies at different initial conditions
-ratio (d) for the optimal reorientation strategies at different initial conditions  in the whole range up to
in the whole range up to  . Solid brown lines indicate the results for a pure Lévy walk with
. Solid brown lines indicate the results for a pure Lévy walk with  . Note that, regardless
. Note that, regardless  , Lévy reorientation strategies show the largest search efficiency compared to the other reorientation strategies, though truncation decreases the efficiency when reaching the symmetric limit
, Lévy reorientation strategies show the largest search efficiency compared to the other reorientation strategies, though truncation decreases the efficiency when reaching the symmetric limit  .
.References
-
- Kamil AC, Sargent TD, editors (1981) Foraging Behavior: Ecological, Ethological, and Psychological Approaches. Garland Series in Ethology, Garland STPM Press, New York.
-
- Kamil AC, Krebs JR, Pulliam HR, editors (1987) Foraging Behavior. Plenum Press, New York.
-
- Shoener TW (1987) A brief history of optimal foraging ecology. In: Kamil AC, Krebs JR, Pulliam H, editors, Foraging Behavior, Plenum Press, New York. pp.5–67.
-
- Krebs JR, Davies NB (1993) An Introduction to Behavioural Ecology. Blackwell, Oxford (3rd ed).
-
- Stephens DW (2007) Models of inofrmation use. In: Stephens DW, Brown JS, Ydenberg RC, editors, Foraging: Behaviour and Ecology, The University of Chicago Press. Chicago, USA. pp.31–58.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

