TLS from fundamentals to practice
- PMID: 25249713
- PMCID: PMC4170067
- DOI: 10.1080/0889311X.2013.835806
TLS from fundamentals to practice
Abstract
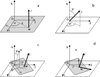
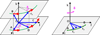
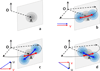
The Translation-Libration-Screw-rotation (TLS) model of rigid-body harmonic displacements introduced in crystallography by Schomaker & Trueblood (1968) is now a routine tool in macromolecular studies and is a feature of most modern crystallographic structure refinement packages. In this review we consider a number of simple examples that illustrate important features of the TLS model. Based on these examples simplified formulae are given for several special cases that may occur in structure modeling and refinement. The derivation of general TLS formulae from basic principles is also provided. This manuscript describes the principles of TLS modeling, as well as some select algorithmic details for practical application. An extensive list of applications references as examples of TLS in macromolecular crystallography refinement is provided.
Keywords: ADP; TLS; atomic displacement parameter; rigid body motion; structure refinement; translation libration screw model.
Figures

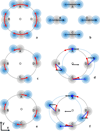
References
-
- Debay P. Interferenz von Röntgenstrahlen und Wärmebewegung (in German) Ann. d. Phys. 1913;348:49–92. (1913).
-
- Johnson CK, Levy HA. Thermal-Motion Analysis Using Bragg Diffraction Data. In: Ibers JA, Hamilton WC, editors. International Tables for X-ray Crystallography. IV. Birmingham: Kynoch Press; 1974. pp. 311–336.
-
- Johnson CK. Thermal motion analysis. In: Diamond R, Ramaseshan S, Venkatesan K, editors. Computing in Crystallography. Bangalor, India: Indian Academy of Sciences; 1980. pp. 14.01–14.19.
-
- Trueblood KN, Bürgi H-B, Burzlaff H, Dunitz JD, Grammaccioli CM, Schulz HH, Shmueli U, Abrahams SC. Atomic displacement parameter nomenclature. Report of a subcommittee on atomic displacement parameter nomenclature. Acta Cryst. 1996;A52:770–781.
-
- Coppens P. The structure factor. In: Shmueli U, editor. International Tables for Crystallography. B. Dordrecht/Boston/London: Kluwer Academic Publishers; 2006. pp. 10–24.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
