On the complexity of Minimum Path Cover with Subpath Constraints for multi-assembly
- PMID: 25252805
- PMCID: PMC4168716
- DOI: 10.1186/1471-2105-15-S9-S5
On the complexity of Minimum Path Cover with Subpath Constraints for multi-assembly
Abstract
Background: Multi-assembly problems have gathered much attention in the last years, as Next-Generation Sequencing technologies have started being applied to mixed settings, such as reads from the transcriptome (RNA-Seq), or from viral quasi-species. One classical model that has resurfaced in many multi-assembly methods (e.g. in Cufflinks, ShoRAH, BRANCH, CLASS) is the Minimum Path Cover (MPC) Problem, which asks for the minimum number of directed paths that cover all the nodes of a directed acyclic graph. The MPC Problem is highly popular because the acyclicity of the graph ensures its polynomial-time solvability.
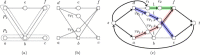
Results: In this paper, we consider two generalizations of it dealing with integrating constraints arising from long reads or paired-end reads; these extensions have also been considered by two recent methods, but not fully solved. More specifically, we study the two problems where also a set of subpaths, or pairs of subpaths, of the graph have to be entirely covered by some path in the MPC. We show that in the case of long reads (subpaths), the generalized problem can be solved in polynomial-time by a reduction to the classical MPC Problem. We also consider the weighted case, and show that it can be solved in polynomial-time by a reduction to a min-cost circulation problem. As a side result, we also improve the time complexity of the classical minimum weight MPC Problem. In the case of paired-end reads (pairs of subpaths), the generalized problem becomes NP-hard, but we show that it is fixed-parameter tractable (FPT) in the total number of constraints. This computational dichotomy between long reads and paired-end reads is also a general insight into multi-assembly problems.
Figures

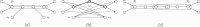

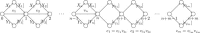
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

